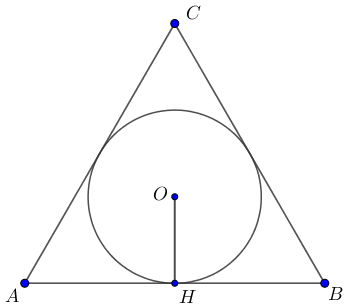
Сначала найдем высоту равностороннего треугольника со стороной \(\displaystyle a\small,\) а затем найдем радиус вписанной окружности.
Проведем высоту \(\displaystyle CH\) равностороннего треугольника \(\displaystyle ABC \small.\)
Так как высота \(\displaystyle CH\) равностороннего треугольника является и его медианой, то
\(\displaystyle AH=\frac{1}{2} \cdot AB=\frac{a}{2} \small.\)
Найдем длину отрезка \(\displaystyle CH\) из прямоугольного треугольника \(\displaystyle ACH \small.\)
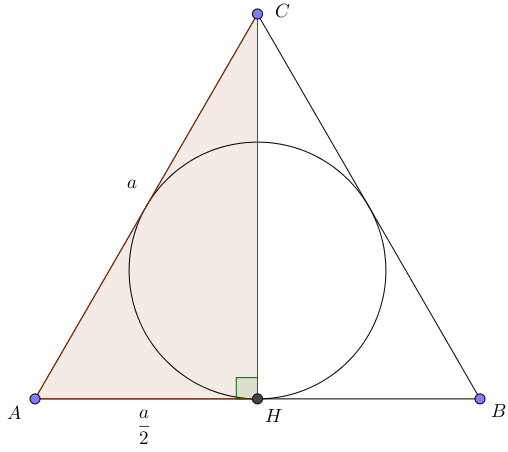 | По теореме Пифагора \(\displaystyle AC^2=AH^2+CH^2 \small.\) Тогда \(\displaystyle CH^2=AC^2-AH^2 \small,\) \(\displaystyle CH^2=a^2-\left( \frac{a}{2}\right)^2=a^2-\frac{a^2}{4}=\frac{3a^2}{4}\small.\) Поскольку длина отрезка положительна, то \(\displaystyle CH=\frac{a\sqrt{3}}{2} \small.\) |
Пусть точка \(\displaystyle O\) – центр вписанной окружности.
Центр вписанной в треугольник окружности – точка пересечения биссектрис.
Биссектрисы равностороннего треугольника являются также высотами. Значит, точка \(\displaystyle O\) лежит на высоте \(\displaystyle CH \small.\) Поскольку отрезок \(\displaystyle OH\) перпендикулярен основанию треугольника, то он является радиусом окружности.
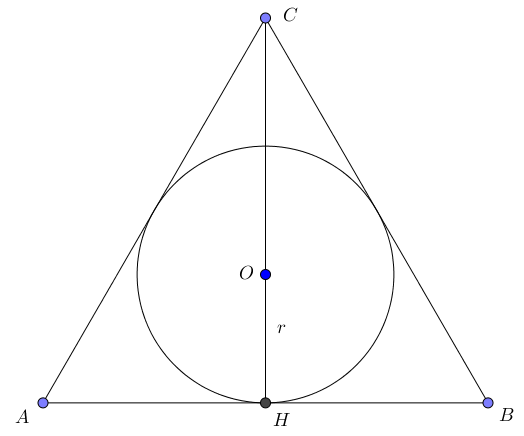
Высота равностороннего треугольника является также медианой, значит точка \(\displaystyle O\) – точка пересечения медиан.
Тогда точка \(\displaystyle O\) делит медиану \(\displaystyle CH\) в отношении \(\displaystyle 2:1 \small,\) считая от вершины \(\displaystyle C \small.\)
Следовательно,
\(\displaystyle r=\frac{1}{3} \cdot CH=\frac{1}{3} \cdot \frac{a\sqrt{3}}{2}=\frac{a\sqrt{3}}{6} \small.\)