В треугольнике \(\displaystyle ABC\) известно, что \(\displaystyle AC=BC{\small , }\) \(\displaystyle AH\) – высота и \(\displaystyle \cos\angle BAC=\frac{7}{25}.\)
Найдите \(\displaystyle \cos\angle HAB.\)
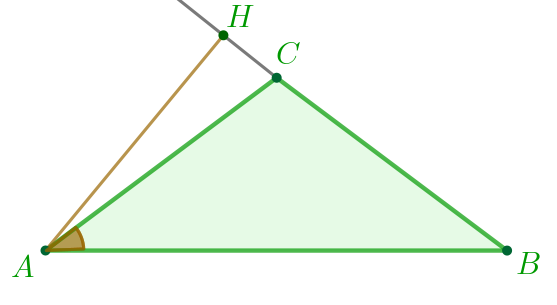
Треугольник \(\displaystyle ABC\) равнобедренный. Следовательно, \(\displaystyle \cos\angle BAC=\cos\angle CBA{\small.}\)
Пусть \(\displaystyle \angle BAC= \alpha\) и \(\displaystyle \cos \alpha=\frac{7}{25}{\small.}\) | 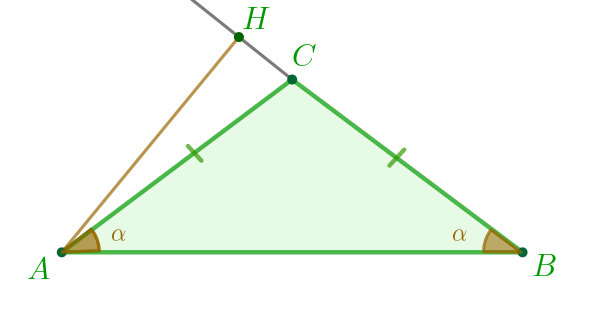 |
Рассмотрим прямоугольный треугольник \(\displaystyle ABH{\small.}\)
По определению косинуса в прямоугольном треугольнике: \(\displaystyle \cos \alpha=\frac{HB}{AB}{\small.}\) По определению синуса в прямоугольном треугольнике: \(\displaystyle \sin \angle HAB=\frac{HB}{AB}{\small.}\) | 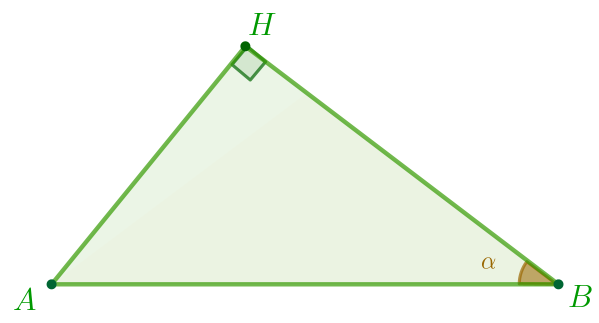 |
Значит,
\(\displaystyle \sin \angle HAB=\cos \alpha=\frac{7}{25}{\small.}\)
Для нахождения \(\displaystyle \cos\angle HAB\) воспользуемся основным тригонометрическим тождеством:
\(\displaystyle \sin^2\angle HAB+\cos^2 \angle HAB=1{\small;}\)
\(\displaystyle \cos^2\angle HAB = 1 - \sin^2\angle HAB{\small.}\)
Подставим \(\displaystyle \sin \angle HAB=\frac{7}{25}{\small:}\)
\(\displaystyle \cos^2\angle HAB=1-\bigg(\frac{7}{25}\bigg)^2{\small;}\)
\(\displaystyle \cos^2\angle HAB=1-\frac{49}{625}{\small;}\)
\(\displaystyle \cos^2\angle HAB=\frac{576}{625}{\small.}\)
Так как угол \(\displaystyle HAB\) – острый, то
\(\displaystyle \cos\angle HAB=\frac{24}{25}{\small ;}\)
\(\displaystyle \cos\angle HAB=0{,}96{\small .}\)
Ответ: \(\displaystyle 0{,}96{\small .}\)