Установите соответствие между неравенствами и их решениями:
| \(\displaystyle \log_3 x\geqslant 2\) | |
| \(\displaystyle \log_3 x\leqslant -2\) | |
| \(\displaystyle \log_3 x\geqslant -2\) | |
| \(\displaystyle \log_3 x\leqslant 2\) |
Каждое решение соответствует одному из неравенств в условии.
Найдем решения трех неравенств.
Последнему оставшемуся неравенству будет соответствовать оставшееся решение.
Логарифм \(\displaystyle \log_3 x\) определен при \(\displaystyle x>0{\small .}\)
Перепишем правую часть неравенства \(\displaystyle \log_3 x\geqslant 2\) в виде логарифма с основанием \(\displaystyle 3{\small :}\)
\(\displaystyle 2= \log_\color{blue}{3}{3^2}=\log_\color{blue}{3}{9}{\small .}\)
Получим неравенство
\(\displaystyle \log_\color{blue}{3}{x}\geqslant \log_\color{blue}{3}{9}{\small .}\)
Основания логарифмов левой и правой частей равны \(\displaystyle \color{blue}{ 3}{ \small ,}\) при этом \(\displaystyle \color{blue}{ 3}>1{ \small .}\) Тогда при переходе к неравенству на выражения под логарифмом знак неравенства не изменится. Получаем:
\(\displaystyle x\geqslant 9{\small .}\)
С учетом области определения \(\displaystyle x>0{\small ,}\) получаем:
\(\displaystyle \quad\quad\quad\quad\quad\quad\quad\quad\color{red}{x>0}\quad\quad\quad\quad\quad\color{green}{x\geqslant 9}\)
Решением является область с двойной штриховкой. Следовательно,
\(\displaystyle x\geqslant 9{\small .}\)

Следовательно, оставшемуся неравенству \(\displaystyle \log_3 x\leqslant -2\) соответствует единственное оставшееся решение:

Ответ: соответствие между неравенствами и их решениями
| \(\displaystyle \log_3 x\geqslant 2\) |  |
| \(\displaystyle \log_3 x\leqslant -2\) |  |
| \(\displaystyle \log_3 x\geqslant -2\) |  |
| \(\displaystyle \log_3 x\leqslant 2\) |  |
Можно явно показать, что решением неравенства \(\displaystyle \log_3 x\leqslant -2\) является
 .
.
Логарифм \(\displaystyle \log_3 x\) определен при \(\displaystyle x>0{\small .}\)
Перепишем правую часть неравенства \(\displaystyle \log_3 x\leqslant -2\) в виде логарифма с основанием \(\displaystyle 3{\small :}\)
\(\displaystyle -2= \log_\color{blue}{3}{3^{-2}}=\log_\color{blue}{3}{\frac{1}{9}}{\small .}\)
Получим неравенство
\(\displaystyle \log_\color{blue}{3}{x}\leqslant \log_\color{blue}{3}{\frac{1}{9}}{\small .}\)
Основания логарифмов левой и правой частей равны \(\displaystyle \color{blue}{ 3}{ \small ,}\) при этом \(\displaystyle \color{blue}{ 3}>1{ \small .}\) Тогда при переходе к неравенству на выражения под логарифмом знак неравенства не изменится. Получаем:
\(\displaystyle x\leqslant \frac{1}{9}{\small .}\)
С учетом области определения \(\displaystyle x>0{\small ,}\) получаем:
\(\displaystyle \quad\quad\quad\quad\color{green}{x\leqslant \frac{1}{9}}\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\color{red}{x>0}\)
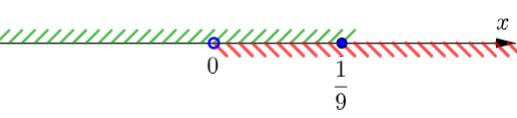
Решением является область с двойной штриховкой. Следовательно,
\(\displaystyle 0<x\leqslant \frac{1}{9}{\small .}\)
