В основании пирамиды \(\displaystyle SABCD\) лежит прямоугольник \(\displaystyle ABCD\) со сторонами \(\displaystyle AB=3 \) и \(\displaystyle BC=2{\small.}\) Известны длины боковых рёбер пирамиды: \(\displaystyle SA=4\sqrt{2} {\small,}\) \(\displaystyle SB=\sqrt{41}{\small,}\) \(\displaystyle SD=6{\small.}\)
\(\displaystyle а)\) Докажите, что \(\displaystyle SA\) – высота пирамиды.
\(\displaystyle б)\) Найдите тангенс угла между плоскостью \(\displaystyle ASD\) и прямой \(\displaystyle SO{\small,}\) где \(\displaystyle O\) – точка пересечения диагоналей прямоугольника \(\displaystyle ABCD{\small.}\)
По условию задачи выполним чертёж.
\(\displaystyle SABCD\) – пирамида, \(\displaystyle ABCD\) – прямоугольник со сторонами \(\displaystyle AB=3 \) и \(\displaystyle BC=2{\small,}\) боковые рёбра: \(\displaystyle SA=4\sqrt{2} {\small,}\) \(\displaystyle SB=\sqrt{41}{\small,}\) \(\displaystyle SD=6{\small.}\) |
\(\displaystyle а)\) Требуется доказать, что \(\displaystyle SA\) – высота пирамиды.
То есть нужно доказать, что ребро \(\displaystyle SA\) перпендикулярно плоскости основания \(\displaystyle ABD{\small.}\)
Признак перпендикулярности прямой и плоскости
Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости: Если
то \(\displaystyle a \perp \alpha{\small.}\) | 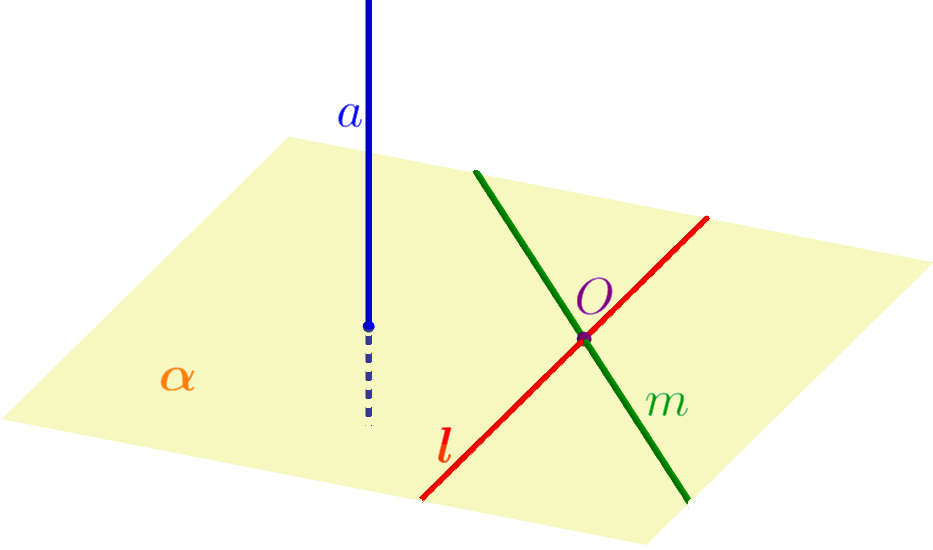 |
Так как \(\displaystyle SA \perp AD\) и \(\displaystyle SA \perp AB{\small,}\) то по признаку перпендикулярности прямой и плоскости, прямая \(\displaystyle SA\) перпендикулярна плоскости \(\displaystyle ABD {\small,}\) то есть \(\displaystyle SA\) является высостой пирамиды \(\displaystyle SABCD {\small,}\) что и требовалось доказать.
|
\(\displaystyle б)\) Требуется найти тангенс угла между плоскостью \(\displaystyle ASD\) и прямой \(\displaystyle SO{\small,}\) где \(\displaystyle O\) – точка пересечения диагоналей прямоугольника \(\displaystyle ABCD{\small.}\)
Угол между прямой и плоскостью
| Углом между прямой и плоскостью, пересекающей эту прямую и не перпендикулярной к ней, называется угол между прямой и ее проекцией на данную плоскость. | 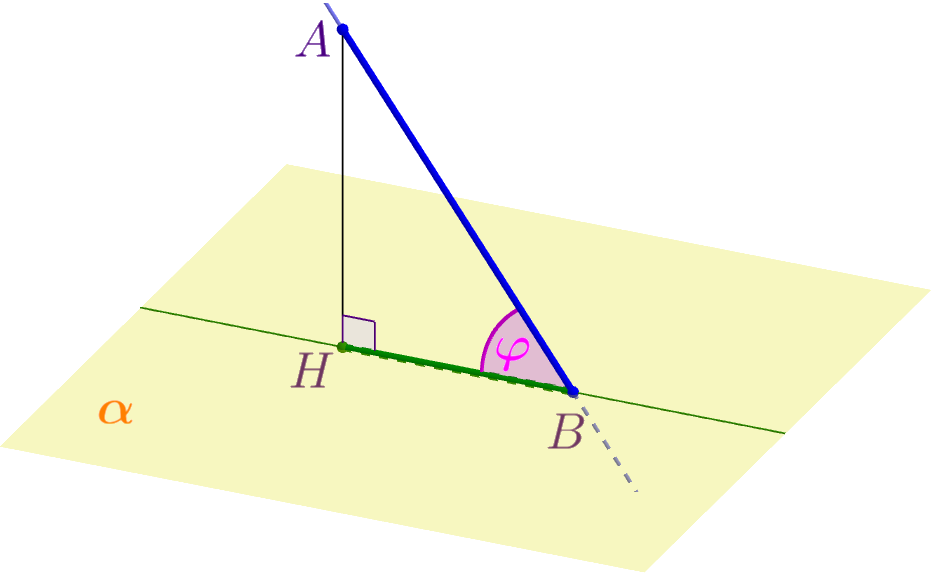 |
Построим проекцию прямой \(\displaystyle SO\) на плоскость \(\displaystyle ASD{\small.}\)
Пусть \(\displaystyle OK\) – перпендикуляр к \(\displaystyle AD{\small.}\) Так как \(\displaystyle OK \perp AD\) и \(\displaystyle OK \perp SA{\small,}\) то по признаку перпендикулярности прямой и плоскости прямая \(\displaystyle OK\) перпендикулярна плоскости \(\displaystyle ASD{\small.}\) Следовательно, \(\displaystyle K\) – проекция точки \(\displaystyle O\) на плоскость \(\displaystyle ASD{\small.}\) Значит, искомый угол между прямой \(\displaystyle SO\) и плоскостью \(\displaystyle ASD\) – это угол \(\displaystyle OSK{\small.}\) |
Получаем
\(\displaystyle \tg \angle OSK=\frac{OK}{SK}=\frac{3}{2\sqrt{33}}=\frac{3 \cdot \sqrt{33}}{2\sqrt{33}\cdot \sqrt{33}}=\frac{3 \cdot \sqrt{33}}{2 \cdot 33}=\frac{\sqrt{33}}{22}{\small.}\)
Ответ: \(\displaystyle \frac{\sqrt{33}}{22}{\small.}\)