В правильной четырёхугольной призме \(\displaystyle ABCDA_1B_1C_1D_1\) стороны основания равны \(\displaystyle 4{\small,}\) а боковые рёбра равны \(\displaystyle 12{\small.}\) Точка \(\displaystyle O\) – центр основания \(\displaystyle ABCD\) призмы.
\(\displaystyle а)\) Докажите, что прямые \(\displaystyle AC\) и \(\displaystyle B_1O\) перпендикулярны.
\(\displaystyle б)\) Найдите синус угла между прямой \(\displaystyle AB_1\) и плоскостью \(\displaystyle BDD_1{\small.}\)
По условию задачи выполним чертёж.
\(\displaystyle ABCDA_1B_1C_1D_1\) – правильная призма, \(\displaystyle ABCD\) – квадрат со стороной \(\displaystyle 4{\small,}\) \(\displaystyle CC_1=12\) – высота призмы, \(\displaystyle O\) – точка пересечения диагоналей \(\displaystyle AC\) и \(\displaystyle BD \) основания \(\displaystyle ABCD{\small.}\) |
\(\displaystyle а) \) Требуется доказать, что прямые \(\displaystyle AC\) и \(\displaystyle B_1O \) перпендикулярны.
Доказательство:
Способ \(\displaystyle 1\)
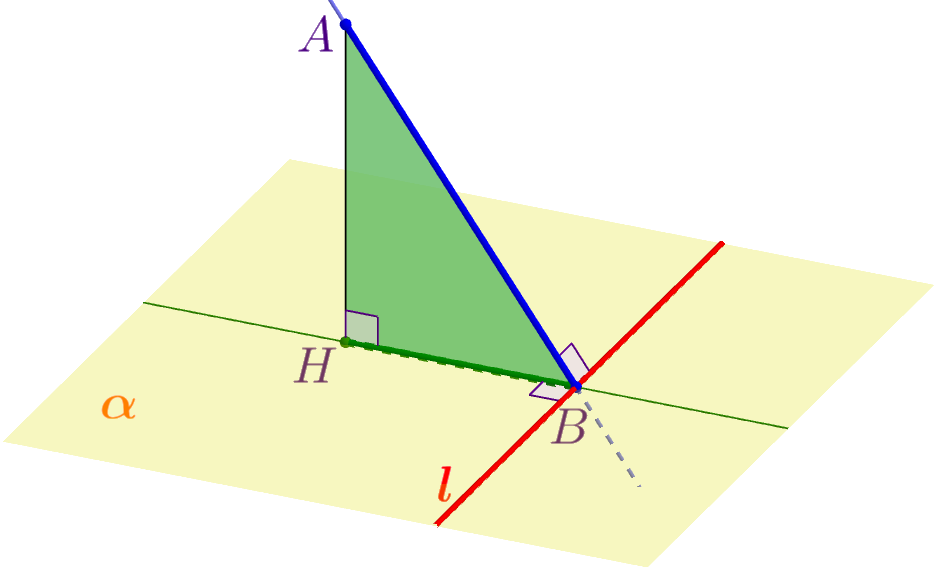
- По определению правильной призмы ребро \(\displaystyle B_1B\) перпендикулярно плоскости основания \(\displaystyle ABCD{\small.}\) Следовательно, \(\displaystyle BO\) – проекция \(\displaystyle B_1O\) на плоскость \(\displaystyle ABC{\small.}\)
- Диагонали квадрата перпендикулярны. Значит, \(\displaystyle BO \perp AC {\small.}\)
Способ \(\displaystyle 2\)
Прямоугольные треугольники \(\displaystyle ABB_1\) и \(\displaystyle CBB_1\) равны по двум катетам:
Следовательно, гипотенузы данных треугольников равны: \(\displaystyle AB_1=CB_1{\small.}\) |
Рассмотрим треугольник \(\displaystyle AB_1C{\small:}\)
Значит, \(\displaystyle B_1O\) – медиана равнобедренного треугольника \(\displaystyle AB_1C{\small.}\) |
По свойству равнобедренного треугольника медиана, проведенная к основанию, является высотой данного треугольника. Следовательно,
\(\displaystyle B_1O \perp AC{\small.}\)
Способ \(\displaystyle 3\)
Признак перпендикулярности прямой и плоскости
Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости: Если
то \(\displaystyle a \perp \alpha{\small.}\) | 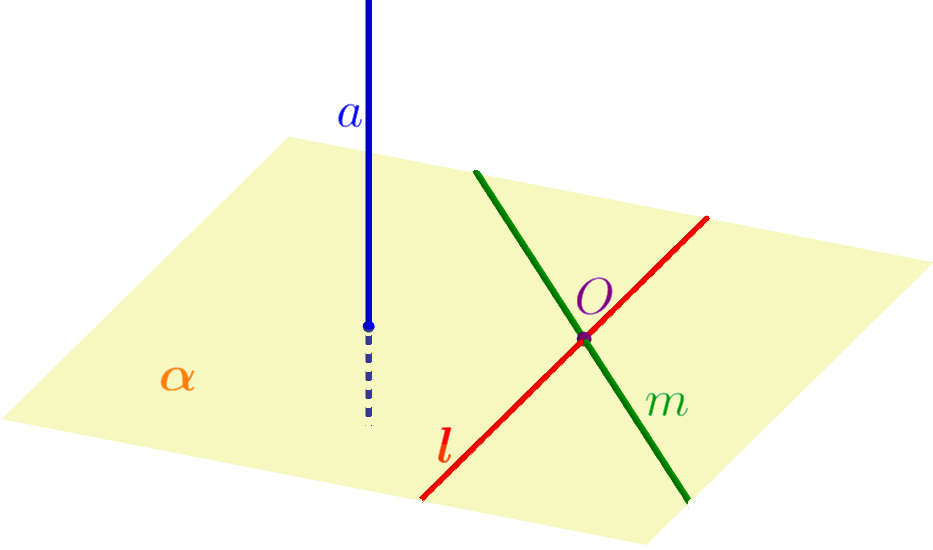 |
Так как \(\displaystyle AO \perp BD\) и \(\displaystyle AO \perp BB_1{\small,}\) то по признаку перпендикулярности прямой и плоскости прямая \(\displaystyle AO\) перпендикулярна плоскости \(\displaystyle BDD_1{\small.}\) Значит, \(\displaystyle AO\) перпендикулярна любой прямой, лежащей в плоскости \(\displaystyle BDD_1{\small.}\) Прямая \(\displaystyle B_1O\) лежит в плоскости \(\displaystyle BDD_1{\small.}\) Следовательно, \(\displaystyle B_1O \perp AO{\small.}\) Значит,
\(\displaystyle B_1O \perp AC{\small.}\)
Утверждение доказано.
\(\displaystyle б)\) Требуется найти синус угла между прямой \(\displaystyle AB_1\) и плоскостью \(\displaystyle BDD_1{\small.}\)
Угол между прямой и плоскостью
| Углом между прямой и плоскостью, пересекающей эту прямую и не перпендикулярной к ней, называется угол между прямой и ее проекцией на данную плоскость. | 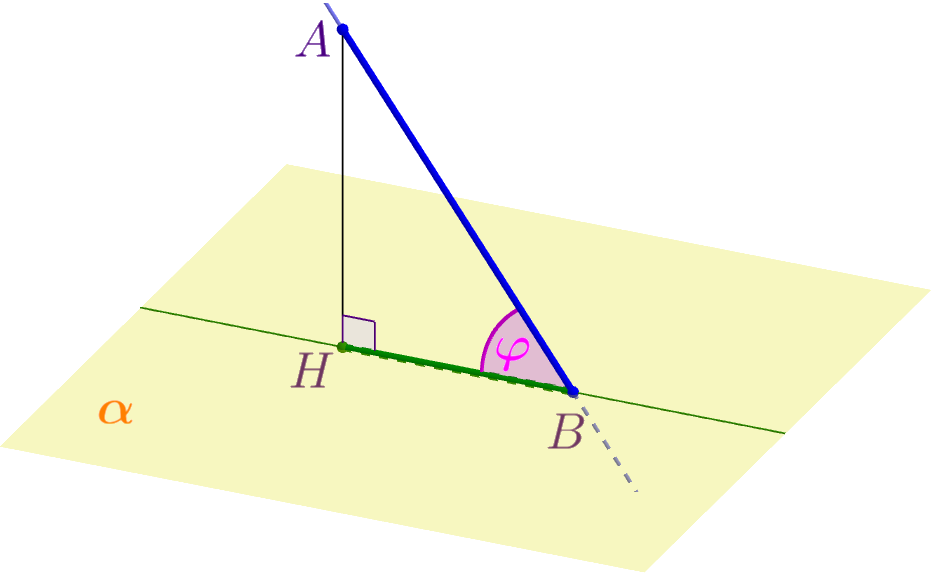 |
Спроецируем \(\displaystyle AB_1\) на плоскость \(\displaystyle BDD_1{\small.}\)
| По доказанному в пункте \(\displaystyle а) \)Способ \(\displaystyle 3\) известно, что прямая \(\displaystyle AO\) перпендикулярна плоскости \(\displaystyle BDD_1{\small.}\) Поэтому проекцией прямой \(\displaystyle AB_1\) на плоскость \(\displaystyle BDD_1 \) является прямая \(\displaystyle OB_1{\small.}\) Следовательно, искомый угол между прямой \(\displaystyle AB_1\) и плоскостью \(\displaystyle BDD_1\) равен углу \(\displaystyle AB_1O{\small.}\) Нужно найти \(\displaystyle \sin {\angle AB_1O} {\small.}\) |
Рассмотрим треугольник \(\displaystyle AB_1O{\small.}\)
Так как \(\displaystyle B_1O \perp AO{\small,}\) то \(\displaystyle \triangle AB_1O \) – прямоугольный. Тогда
\(\displaystyle \sin {\angle AB_1O}= \frac{AO}{AB_1} {\small.}\)
Значит,
\(\displaystyle \sin {\angle AB_1O}= \frac{AO}{AB_1}= \frac{2\sqrt{2}}{4\sqrt{10}}= \frac{1}{2\sqrt{5}} = \frac{\sqrt{5}}{10}{\small.}\)
Ответ: \(\displaystyle \frac{\sqrt{5}}{10}{\small.}\)