Периметр параллелограмма с острым углом \(\displaystyle 30^{\circ}\) равен \(\displaystyle 46 \small.\) Одна сторона параллелограмма на \(\displaystyle 3\) больше другой. Найдите площадь параллелограмма.
Найдем сначала стороны параллелограмма.
Пусть \(\displaystyle AB=x\) – меньшая сторона параллелограмма, тогда \(\displaystyle AD=x+3\) – большая сторона параллелограмма.
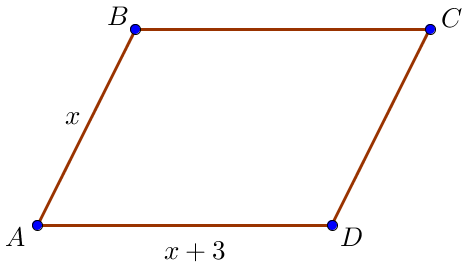
Периметр параллелограмма равен \(\displaystyle P=2\cdot (AB+AD) \small.\) Известно, что \(\displaystyle P=46 \small.\)
Значит,
\(\displaystyle 2\cdot (x+x+3)=46 \small,\)
\(\displaystyle 2\cdot (2x+3)=46 \, | :\color{red}{2} \small,\)
\(\displaystyle 2x+3=23 \small,\)
\(\displaystyle 2x=20 \, | :\color{red}{2} \small,\)
\(\displaystyle x=10 \small.\)
Тогда \(\displaystyle AB=10 \small,\) \(\displaystyle {AD}=10+3=13 \small.\)
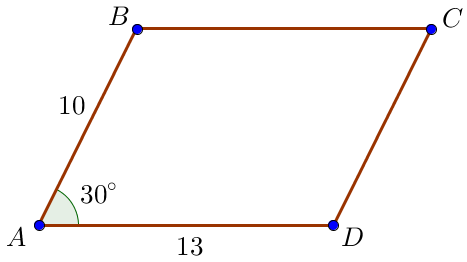
Площадь параллелограмма может быть найдена как произведение смежных сторон на синус угла между ними:
\(\displaystyle {S_{пар}} = {AB}\cdot AD \cdot \sin \angle BAD = {10}\cdot 13\cdot \angle 30^{\circ} = 130 \cdot \frac{1}{2}=65 {\small.}\)
Ответ: \(\displaystyle 65{\small .}\)