Один угол параллелограмма больше другого на \(\displaystyle 104^\circ \small.\) Найдите больший угол. Ответ дайте в градусах.
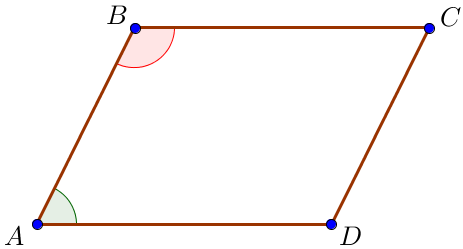
Два угла параллелограмма могут быть прилежащими к одной стороне или противоположными.
По свойству параллелограмма противоположные углы равны,
\(\displaystyle \angle A=\angle C\) и \(\displaystyle \angle B=\angle D \small.\)
Так как по условию один угол параллелограмма больше другого на \(\displaystyle 104^\circ \small,\) то они не являются противоположными. Значит, они прилежат к одной стороне.
Пусть в условии задачи упоминаются прилежащие к одной стороне углы \(\displaystyle \color{red}{ABC}\) и \(\displaystyle \color{green}{BAD} \small.\) Угол \(\displaystyle \color{red}{ABC}\) больше угла \(\displaystyle \color{green}{BAD}\) на \(\displaystyle \color{blue}{104^{\circ}} \small.\)
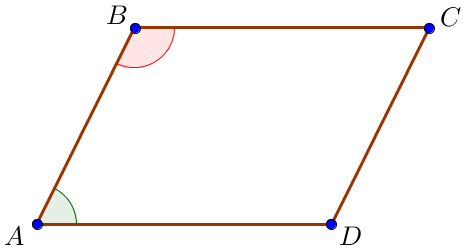
Обозначим \(\displaystyle \color{green}{\angle BAD}=\color{green}{x} \small,\) тогда
\(\displaystyle \color{red}{\angle ABC}=\color{green}{\angle BAD}+\color{blue}{104^{\circ}}=\color{green}{x}+\color{blue}{104} \small.\)
По свойству параллелограмма сумма углов, прилежащих к одной стороне, равна \(\displaystyle 180^\circ \small.\) Значит,
\(\displaystyle \color{green}{\angle BAD}+\color{red}{\angle ABC}= 180^{\circ} \small.\)
Получаем уравнение
\(\displaystyle \color{green}{x}+(\color{red}{x+104})= 180 \small,\)
откуда
\(\displaystyle {2x}+104= 180 \small,\)
\(\displaystyle {2x} = 76 \small,\)
\(\displaystyle {x} = 38 \small.\)
Значит, \(\displaystyle \angle BAD={x}=38^{\circ}{ \small ,} \) откуда \(\displaystyle {\angle ABC}=38+104=142^\circ \small.\)
Следовательно, наибольший угол параллелограмма составляет \(\displaystyle 142^\circ \small.\)
Ответ: \(\displaystyle 142 \small.\)