Найдите больший угол параллелограмма, если два его угла относятся как \(\displaystyle 3 : 7 \small.\) Ответ дайте в градусах.
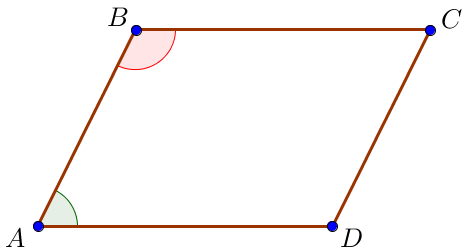
Пусть углы \(\displaystyle \color{green}{BAD}\) и \(\displaystyle \color{red}{ABC}\) относятся как \(\displaystyle \color{blue}{3 : 7} \small,\)
\(\displaystyle \frac{\color{green}{\angle BAD}}{\color{red}{\angle ABC}}=\color{blue}{\frac{3}{7}} \small.\)
Это означает, что если разделить угол \(\displaystyle \color{green}{BAD}\) на \(\displaystyle 3\) равные части, то угол \(\displaystyle \color{red}{ABC}\) можно разделить
на \(\displaystyle 7\) таких же частей.
Обозначим через \(\displaystyle x\) градусную меру одной части. Тогда
\(\displaystyle \color{green}{\angle BAD}=\color{green}{3x}\) и \(\displaystyle \color{red}{\angle ABC}=\color{red}{7x} \small.\)
По свойству параллелограмма, сумма углов, прилежащих к одной стороне, равна \(\displaystyle 180^\circ \small.\) Значит,
\(\displaystyle \color{green}{\angle BAD}+\color{red}{\angle ABC}= 180^{\circ} \small.\)
Получаем уравнение
\(\displaystyle \color{green}{3x}+\color{red}{7x}= 180 \small,\)
откуда
\(\displaystyle {10x}= 180 \small,\)
\(\displaystyle {x} = 18 \small.\)
Тогда \(\displaystyle {\angle BAD}=3\cdot 18=54^\circ,\) \(\displaystyle {\angle ABC}=7\cdot 18=126^\circ \small.\)
Следовательно, наибольший угол параллелограмма составляет \(\displaystyle 126^\circ \small.\)
Ответ: \(\displaystyle 126 \small.\)