Две стороны параллелограмма относятся как \(\displaystyle 3 : 4 \small,\) а периметр его равен \(\displaystyle 70 \small.\) Найдите большую сторону параллелограмма.
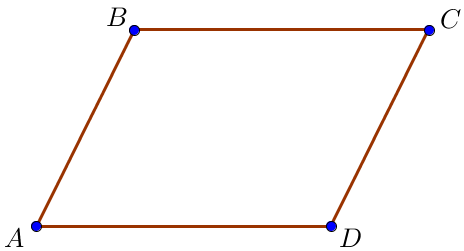
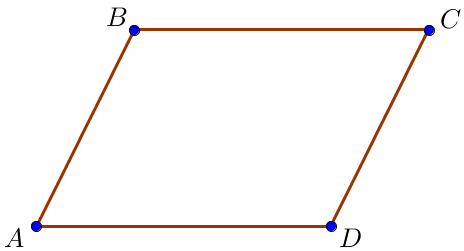
Пусть стороны \(\displaystyle \color{green}{AB}\) и \(\displaystyle \color{red}{AD}\) относятся как \(\displaystyle \color{blue}{3 : 4} \small,\)
\(\displaystyle \frac{\color{green}{AB}}{\color{red}{AD}}=\color{blue}{\frac{3}{4}} \small.\)
Это означает, что если мы разделим отрезок \(\displaystyle AB\) на \(\displaystyle 3\) равные части, то отрезок \(\displaystyle AD\) можно разделить на \(\displaystyle 4\) такие же части.
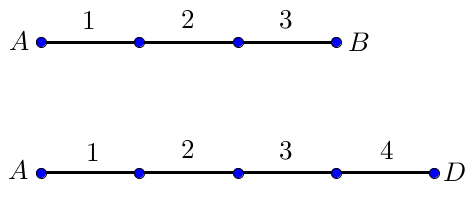
Обозначим через \(\displaystyle x\) длину одной части. Тогда \(\displaystyle \color{green}{AB}=\color{green}{3x} \small,\) \(\displaystyle \color{red}{AD}=\color{red}{4x} \small.\)
По условию задачи, периметр параллелограмма равен \(\displaystyle 70 \small.\) Значит,
\(\displaystyle 2\cdot (\color{green}{ AB}+\color{red}{AD})= 70 \small.\)
Получаем уравнение
\(\displaystyle 2\cdot (\color{green}{3x}+\color{red}{4x})= 70 \small,\)
откуда
\(\displaystyle {2\cdot 7x}= 70 \small,\)
\(\displaystyle {14x}= 70 \small,\)
\(\displaystyle {x} = 5 \small.\)
Тогда \(\displaystyle {AB}=3\cdot 5=15 \small,\) \(\displaystyle {AD}=4\cdot 5=20 \small.\)
Следовательно, большая сторона параллелограмма равна \(\displaystyle 20 \small.\)
Ответ: \(\displaystyle 20\small.\)