Стороны параллелограмма равны \(\displaystyle 4\) и \(\displaystyle 16\small.\) Высота, опущенная на первую из этих сторон, равна \(\displaystyle 36\small.\) Найдите высоту, опущенную на вторую сторону параллелограмма.
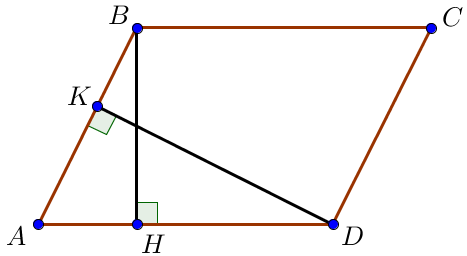
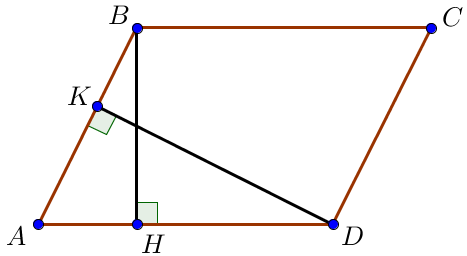
Пусть стороны параллелограмма \(\displaystyle AB=4\) и \(\displaystyle AD=16 \small,\) высота \(\displaystyle DK=36 {\small .}\)
Сначала найдем площадь параллелограмма.
Площадь параллелограмма может быть найдена как произведение основания на высоту:
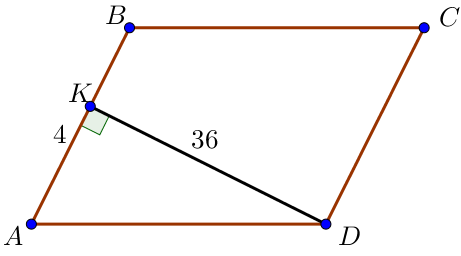
\(\displaystyle {S_{пар}} = {AB}\cdot DK = {4}\cdot 36 = 144 {\small.}\)
С другой стороны,
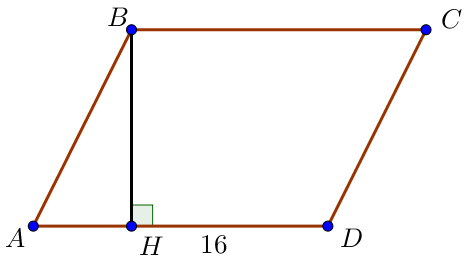
\(\displaystyle {S_{пар}} = {AD}\cdot BH {\small.}\)
Значит,
\(\displaystyle 144 = {16}\cdot BH {\small ,}\)
\(\displaystyle BH = \frac{144}{16}=9 {\small .}\)
Ответ: \(\displaystyle 9{\small .}\)