Диагонали ромба относятся как \(\displaystyle 3 : 4{\small .}\) Периметр ромба равен \(\displaystyle 200{\small .}\) Найдите высоту ромба.
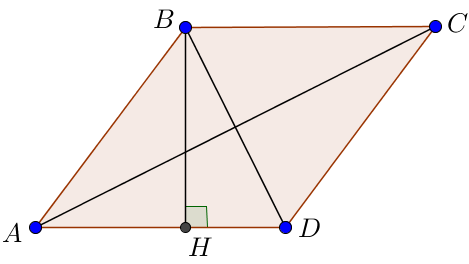
План решения задачи
1. Найдем сторону ромба.
2. Найдем диагонали ромба.
3. Найдем площадь ромба.
4. Найдем высоту.
1. Поскольку периметр ромба вычисляется по формуле \(\displaystyle P=4 \cdot AB{\small ,}\) то
\(\displaystyle 200=4\cdot AB{\small ,}\)
\(\displaystyle AB=\frac{200}{4}=50{\small .}\)
2. Пусть \(\displaystyle BD:AC=3:4{\small .}\) Это означает, что если мы разделим отрезок \(\displaystyle BD\) на \(\displaystyle 3\) равные части, то отрезок \(\displaystyle AC\) можно разделить на \(\displaystyle 4\) такие же части.
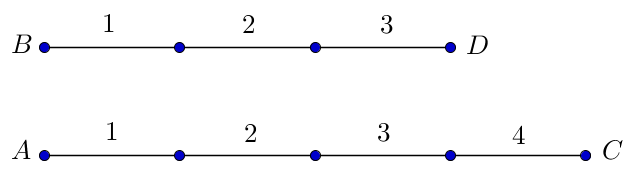
Обозначим через \(\displaystyle x\) длину одной части. Тогда \(\displaystyle BD=3x{\small ,}\) а \(\displaystyle AC=4x{\small .}\)
Пусть \(\displaystyle O\) – точка пересечения диагоналей ромба \(\displaystyle ABCD{\small .}\)

По свойству параллелограмма диагонали точкой пересечения делятся пополам. Значит,
\(\displaystyle AO=OC=2x\) и \(\displaystyle BO=OD=\frac{3x}{2}{\small .}\)
По свойству ромба диагонали перпендикулярны.
Значит, угол \(\displaystyle AOB\) – прямой.
В прямоугольном треугольнике \(\displaystyle AOB\) по теореме Пифагора

\(\displaystyle AB^2=AO^2+OB^2{\small .}\)
Тогда
\(\displaystyle (50)^2=(2x)^2+\left(\frac{3x}{2}\right)^2{\small ,}\)
\(\displaystyle 2500=4x^2+\frac{9x^2}{4}{\small ,}\)
\(\displaystyle 2500=\frac{16x^2+9x^2}{4}{\small ,}\)
\(\displaystyle 2500=\frac{25x^2}{4}{\small .}\)
Получаем:
\(\displaystyle x^2=\frac{2500\cdot 4}{25}{\small ,}\)
\(\displaystyle x^2=400{\small .}\)
Поскольку длина отрезка положительна, то
\(\displaystyle x=20{\small .}\)
Тогда \(\displaystyle BD=3x=60{\small ,}\) \(\displaystyle AC=4x=80{\small .}\)
3. Поскольку площадь ромба равна половине произведения диагоналей
\(\displaystyle S=\frac{1}{2}\cdot AC\cdot BD {\small ,}\)
то
\(\displaystyle S=\frac{1}{2}\cdot 80\cdot 60 =2400{\small .}\)
4. С другой стороны, площадь ромба равна произведению высоты \(\displaystyle BH\) на сторону \(\displaystyle AD{\small : } \)
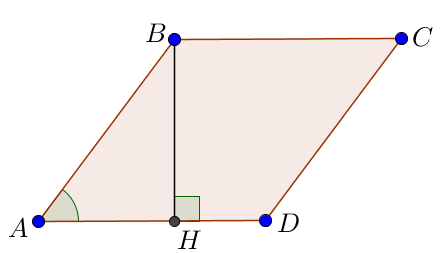
\(\displaystyle {S_{ромб}} = {BH }\cdot AD {\small.}\)
Тогда
\(\displaystyle {2400} = {BH }\cdot 50 {\small ,}\)
\(\displaystyle {BH }= \frac{2400}{50}=48 {\small.}\)
Ответ: \(\displaystyle 48{\small .}\)