Задание
Найдите сторону ромба, высота которого равна \(\displaystyle \sqrt{3}{\small ,}\) а острый угол равен \(\displaystyle 60^\circ{\small .}\)
Решение
Найдем сторону \(\displaystyle AB\) ромба из прямоугольного треугольника \(\displaystyle ABH{\small :}\)
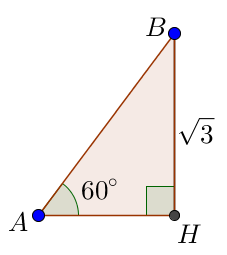
\(\displaystyle BH\) – катет, лежащий против острого угла \(\displaystyle A {\small ,}\) \(\displaystyle AB\) – гипотенуза прямоугольного треугольника \(\displaystyle ABH{\small .}\) Тогда
\(\displaystyle AB=\frac{BH}{\sin A} = \frac{\sqrt{3}}{\sin 60^{\circ}}=\frac{\phantom{1}\sqrt{3}\phantom{1}}{\frac{\sqrt{3}}{2}}=\frac{2\sqrt{3}}{{\sqrt{3}}}={2}.\)
Ответ: \(\displaystyle 2{\small .}\)