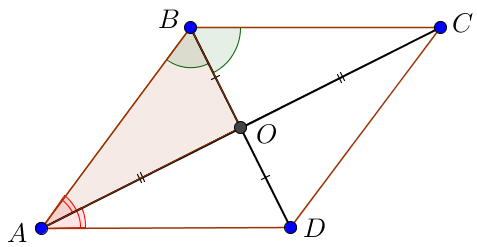
Сторона ромба равна \(\displaystyle 6{\small,}\) а площадь ромба составляет \(\displaystyle 18{\small ,}\) Найдите угол между большей диагональю и стороной ромба. Ответ дайте в градусах.
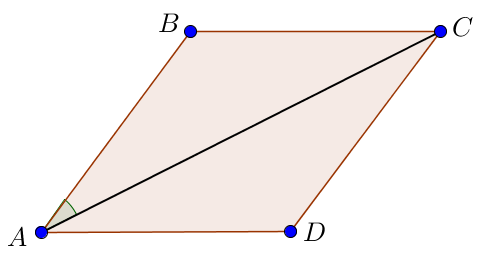
Пусть \(\displaystyle \alpha =\angle BAD\) – острый угол между сторонами ромба.
Известно, что
Требуется найти \(\displaystyle \angle CAB{\small .}\)

Воспользуемся формулой для вычисления площади ромба
\(\displaystyle S_{ромб}=a^2 \sin \alpha {\small ,}\)
где \(\displaystyle a\) – сторона ромба.
В данном случае \(\displaystyle a=6{\small ,}\) \(\displaystyle {S_{ромб}} = 18 {\small : } \)
\(\displaystyle 18 = {6}^2 \cdot \sin \alpha {\small ,}\)
\(\displaystyle 18 = 36 \cdot \sin \alpha {\small .}\)
Тогда
\(\displaystyle \sin \alpha =\frac{18}{36}{\small ,}\)
\(\displaystyle \sin \alpha =\frac{1}{2}{\small .}\)
Поскольку \(\displaystyle \alpha \) – острый угол, то \(\displaystyle \alpha =30^{\circ} {\small .}\)
Так как диагональ ромба является биссектрисой, то \(\displaystyle \angle CAB = \angle CAD = 15^{\circ}{\small .}\)
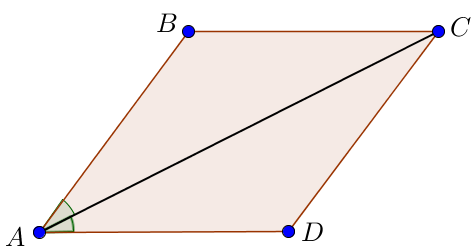
Тогда угол между большей диагональю и стороной ромба составляет \(\displaystyle 15^\circ {\small .}\)
Ответ: \(\displaystyle 15^{\circ}{\small .}\)