Найдите значение выражения:
\(\displaystyle -4 \sqrt{3} \, \cos ({-750^\circ })=\)
Применим формулу \(\displaystyle \cos (-\alpha)=\cos\alpha :\)
\(\displaystyle -4 \sqrt{3} \, \cos ({-750^\circ })=-4 \sqrt{3} \, \cos{750^\circ }{\small .}\)
Поскольку \(\displaystyle 750^\circ=\color{red}{ 4}\cdot 180^\circ+30^\circ,\) то\(\displaystyle 750^\circ \) находится между \(\displaystyle \color{red}{ 4}\cdot 180^\circ \) и \(\displaystyle \color{red}{ 5}\cdot 180^\circ {\small , }\) то есть
\(\displaystyle \color{red}{ 4}\cdot 180^\circ<750^\circ<\color{red}{ 5}\cdot 180^\circ{\small .}\)
Так как
то запишем \(\displaystyle 750^\circ \) следующим образом:
\(\displaystyle 750^\circ =4\cdot 180^\circ+30^\circ{\small ,}\) откуда
\(\displaystyle \cos {750^\circ }=\cos {(4\cdot 180^\circ+30^\circ)}{\small .}\)
Применим формулу приведения.
\(\displaystyle \cos {(4 \cdot 180^\circ+30^\circ)}\)
1. Определим, в какой четверти находится угол \(\displaystyle 4 \cdot 180^\circ+30^\circ:\)
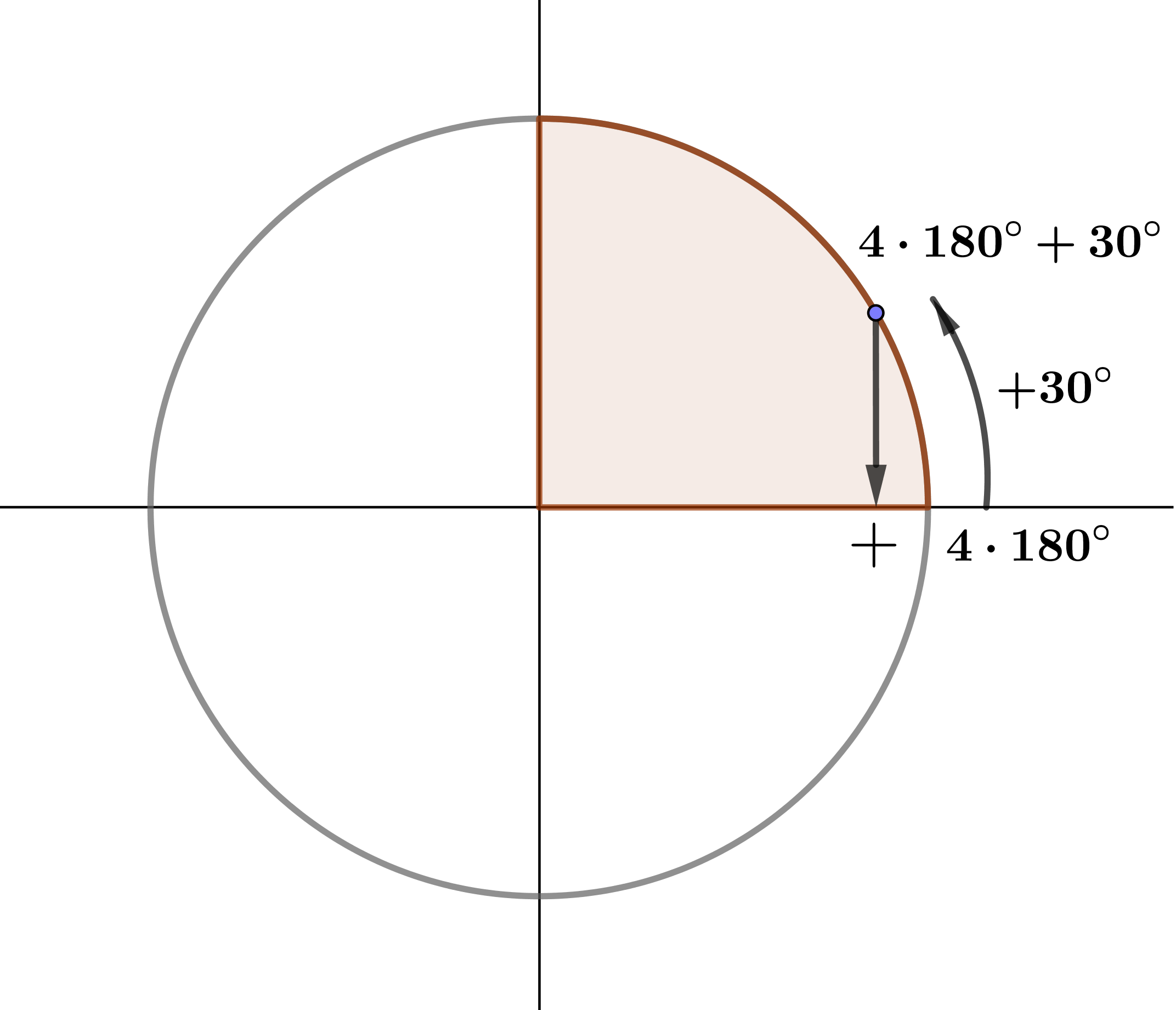
Значит, угол \(\displaystyle 4 \cdot 180^\circ+30^\circ \) находится в первой четверти.
2. Определим знак исходной функции.
В первой четверти косинус положительный (\(\displaystyle {\bf +}\)).
3. Определим, какая будет функция.
Так как к аргументу \(\displaystyle 30^\circ\) прибавляем \(\displaystyle 4 \cdot 180^\circ \) (целое число раз по \(\displaystyle 180^\circ\)), то функция не меняется.
Значит,
\(\displaystyle \cos {(4 \cdot 180^\circ+30^\circ)}=+\cos {30^\circ}\)
или
\(\displaystyle \cos {750^\circ}=\cos {30^\circ}{\small .}\)
А \(\displaystyle \cos 30^\circ\) – это уже табличное значение.
Таким образом, верна следующая цепочка равенств:
\(\displaystyle -4 \sqrt{3} \, \cos (-750^\circ)=-4 \sqrt{3} \, \cos 750^\circ=-4 \sqrt{3} \, \cos 30^\circ=-4 \sqrt{3} \cdot \frac{\sqrt 3}{2} =-\frac{4 \cdot 3}{2}=-6{\small .}\)
Ответ: \(\displaystyle -6 {\small.} \)