Найдите значение выражения:
\(\displaystyle \frac{8}{ \sin{\big(- \frac{27\pi}{4}}\big) \cos{\frac {31\pi}{4}}}=\)
Используем формулу \(\displaystyle \sin{(-\alpha)}=-\sin\alpha:\)
\(\displaystyle \frac{8}{\color{blue}{\sin{\big(- \frac{27\pi}{4}}\big)} \cos{\frac {31\pi}{4}}}=\frac{8}{ \color{blue}{-\sin{\frac{27\pi}{4}}} \cos{\frac {31\pi}{4}}}=-\frac{8}{\sin{\frac{27\pi}{4}} \cos{\frac {31\pi}{4}}}{\small .}\)
Применим формулу приведения по правилу:
1) Определяем четверть, предполагая \(\displaystyle \alpha \in \left(0;\frac{\pi}{2}\right){\small .}\)
2) Определяем знак исходной функции.
3) Определяем, какая функция будет.
Если к углу \(\displaystyle \pm \alpha \) добавляем или вычитаем
- \(\displaystyle \pm\pi ,\, \pm 2\pi ,\, \pm 3\pi,\, \pm 4\pi,\,\ldots\) (целое число \(\displaystyle \pi\)), то функцию не меняем;
- \(\displaystyle \pm\frac{\pi}{2},\, \pm\frac{3\pi}{2},\, \pm\frac{5\pi}{2},\, \pm\frac{7\pi}{2},\, \ldots\) (нечетное число половинок \(\displaystyle \pi\)), то функцию меняем: \(\displaystyle \sin\) \(\displaystyle \leftrightarrow\) \(\displaystyle \cos\) и \(\displaystyle \tg\) \(\displaystyle \leftrightarrow\) \(\displaystyle \ctg{\small .}\)
Получаем:
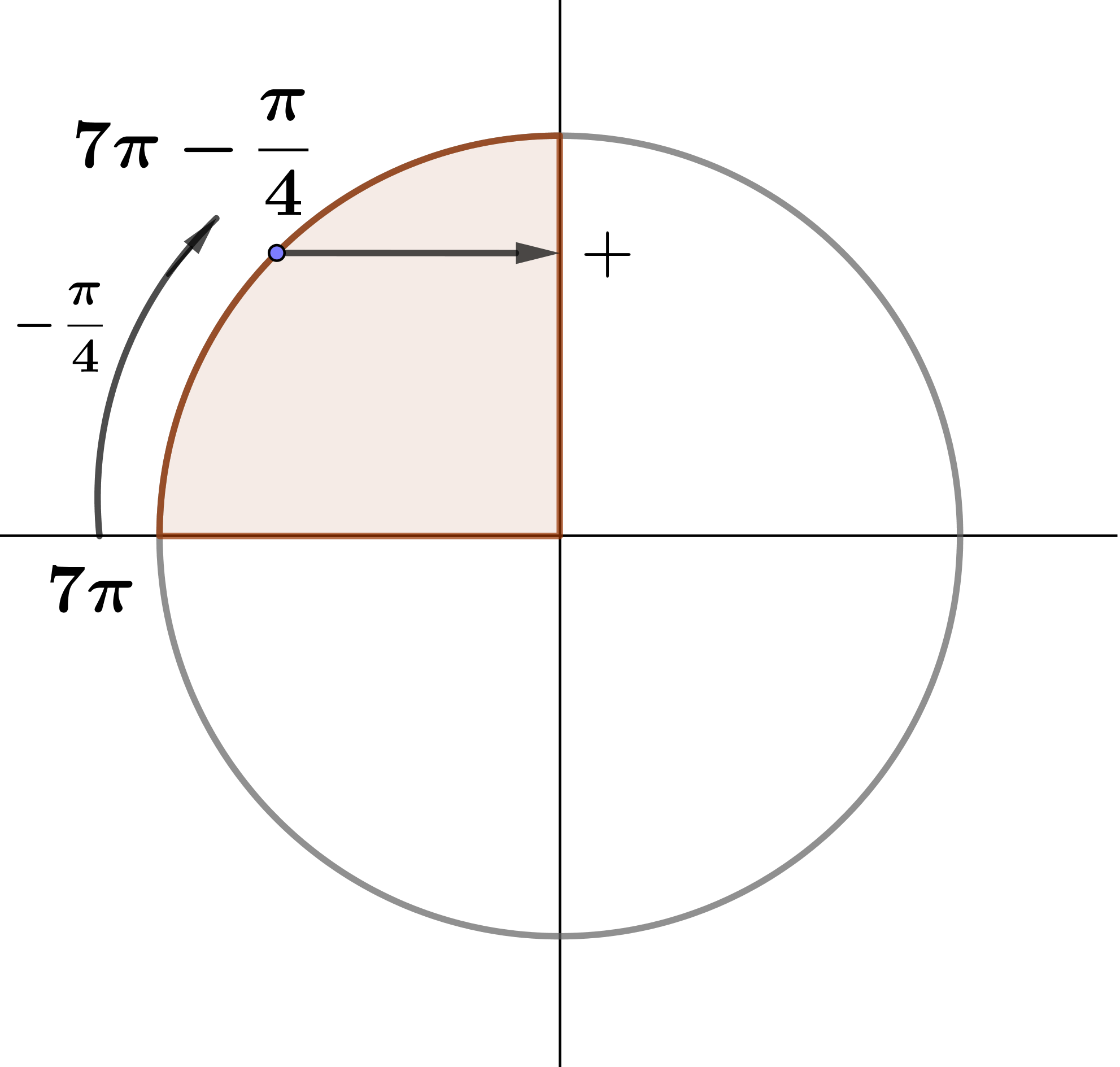
\(\displaystyle \sin {\frac{27\pi}{4}}=\sin {\frac{\pi}{4}}{\small .}\)
Аналогично по формуле приведения определяем:
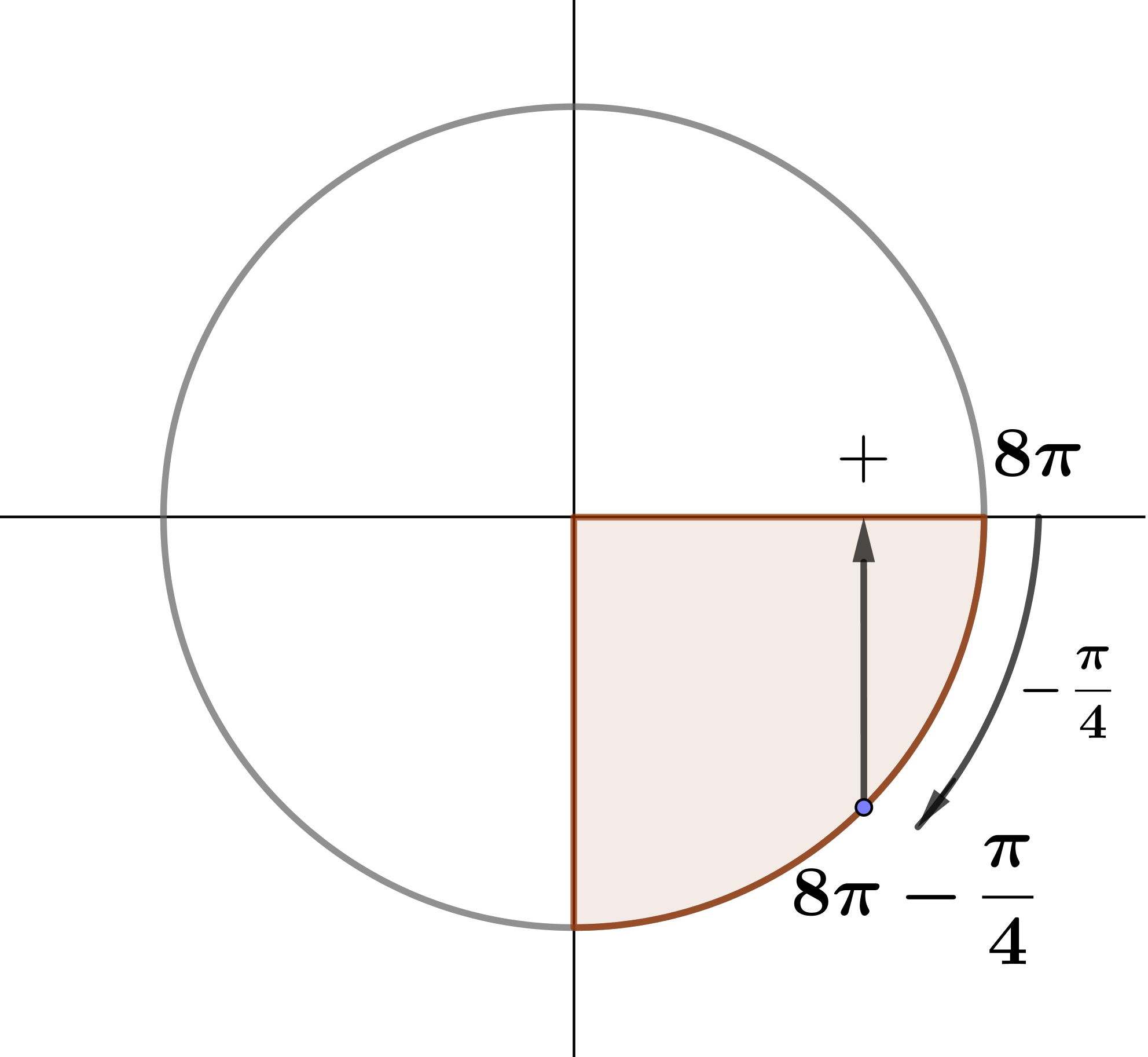
\(\displaystyle \cos {\frac{31\pi}{4}}=\cos {\frac{\pi}{4}}{\small .}\)
\(\displaystyle -\frac{8}{\color{blue}{ \sin{\frac{27\pi}{4}}}\color{green}{ \cos{\frac {31\pi}{4}}}}=-\frac{8}{ \color{blue}{ \sin{ \frac{\pi}{4}}} \color{green}{ \cos{\frac {\pi}{4}}}}{\small .}\)
Подставим табличные значения:
\(\displaystyle -\frac{8}{\color{blue}{\sin{ \frac{\pi}{4}}} \color{green}{\cos{\frac {\pi}{4}}}}=-\frac{8}{\color{blue}{\frac {\sqrt 2}{2}} \cdot \color{green}{\frac {\sqrt 2}{2}}}=-\frac{\phantom{1}8\phantom{1}}{ \frac {1}{2} }= -16{\small .}\)
Таким образом, верна следующая цепочка равенств:
\(\displaystyle \frac{8}{ \sin{\big(- \frac{27\pi}{4}}\big) \cos{\frac {31\pi}{4}}}=-\frac{8}{ \sin{\frac{27\pi}{4}} \cos{\frac {31\pi}{4}}}=-\frac{8}{\sin{ \frac{\pi}{4}} \cos{\frac {\pi}{4}}}=-\frac{8}{\frac {\sqrt 2}{2} \cdot \frac {\sqrt 2}{2}}=-\frac{\phantom{1}8\phantom{1}}{\frac {1}{2} }= -16{\small .}\)
Ответ: \(\displaystyle -16 {\small.} \)