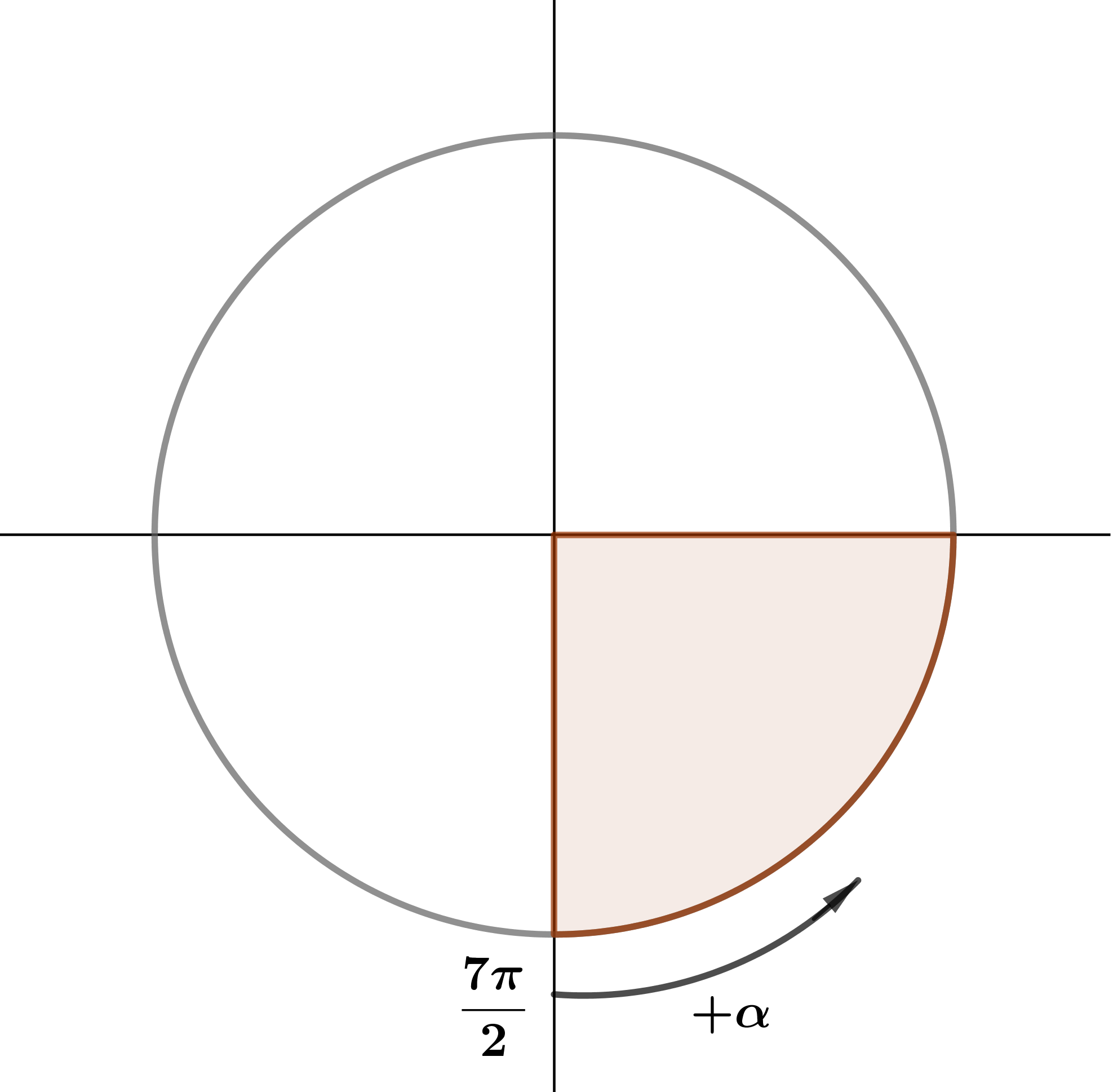
Найдите \(\displaystyle \sin (\alpha +\frac{7\pi}{2}),\) если \(\displaystyle \cos \alpha = 0{,}2{\small .}\)
\(\displaystyle \sin (\alpha +\frac{7\pi}{2})=\)
\(\displaystyle \sin \bigg(\alpha +\frac{7\pi}{2}\bigg)=\sin \bigg(\frac{7\pi}{2}+\alpha \bigg){\small .}\)
Применим формулу приведения по правилу:
1) Определяем четверть, предполагая \(\displaystyle \alpha \in \left(0;\frac{\pi}{2}\right){\small .}\)
2) Определяем знак исходной функции.
3) Определяем, какая функция будет.
Если к углу \(\displaystyle \pm \alpha \) добавляем или вычитаем
- \(\displaystyle \pm\pi ,\, \pm 2\pi ,\, \pm 3\pi,\, \pm 4\pi,\,\ldots\) (целое число \(\displaystyle \pi\)), то функцию не меняем;
- \(\displaystyle \pm\frac{\pi}{2},\, \pm\frac{3\pi}{2},\, \pm\frac{5\pi}{2},\, \pm\frac{7\pi}{2},\, \ldots\) (нечетное число половинок \(\displaystyle \pi\)), то функцию меняем: \(\displaystyle \sin\) \(\displaystyle \leftrightarrow\) \(\displaystyle \cos\) и \(\displaystyle \tg\) \(\displaystyle \leftrightarrow\) \(\displaystyle \ctg{\small .}\)
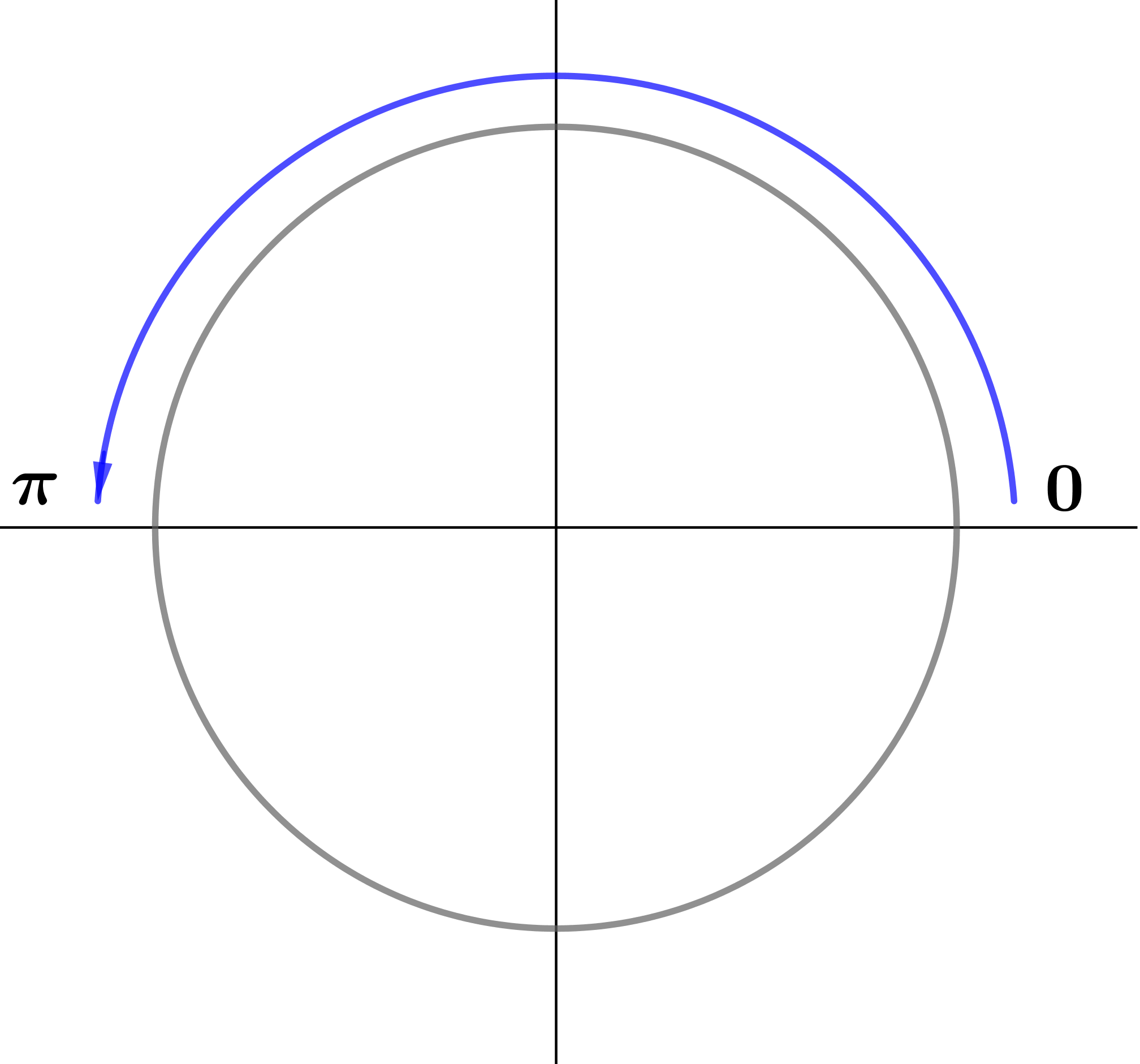
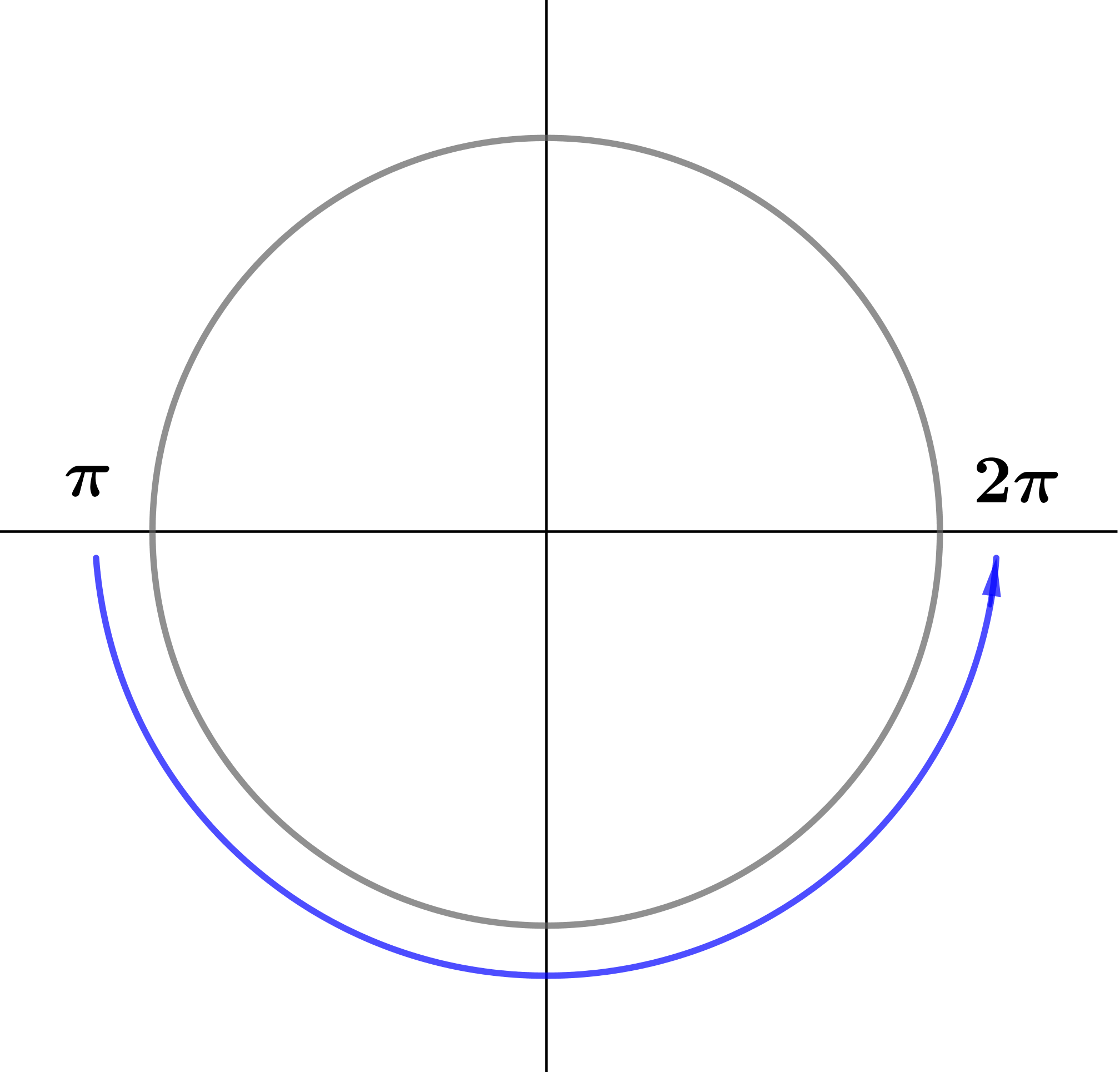
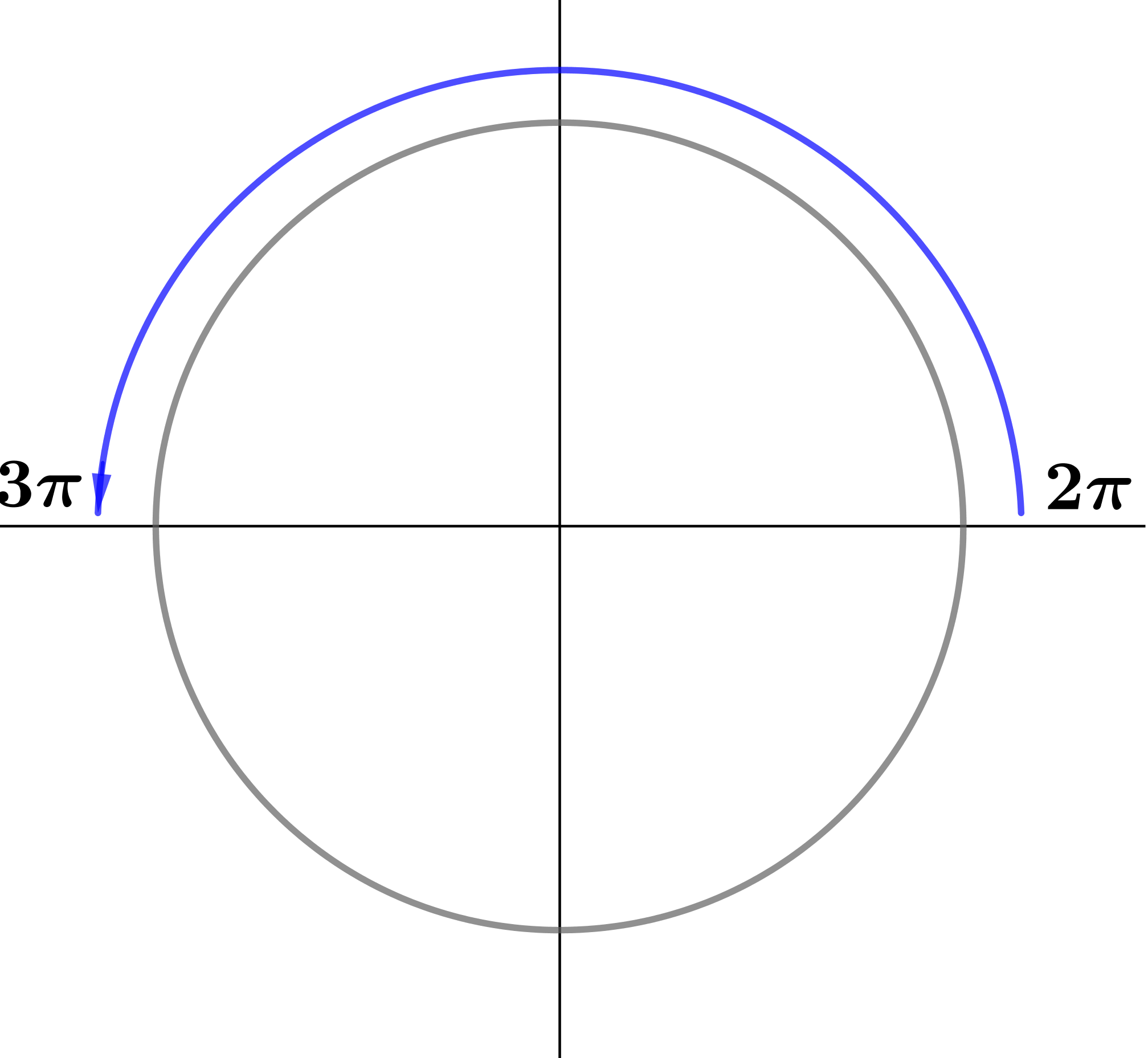
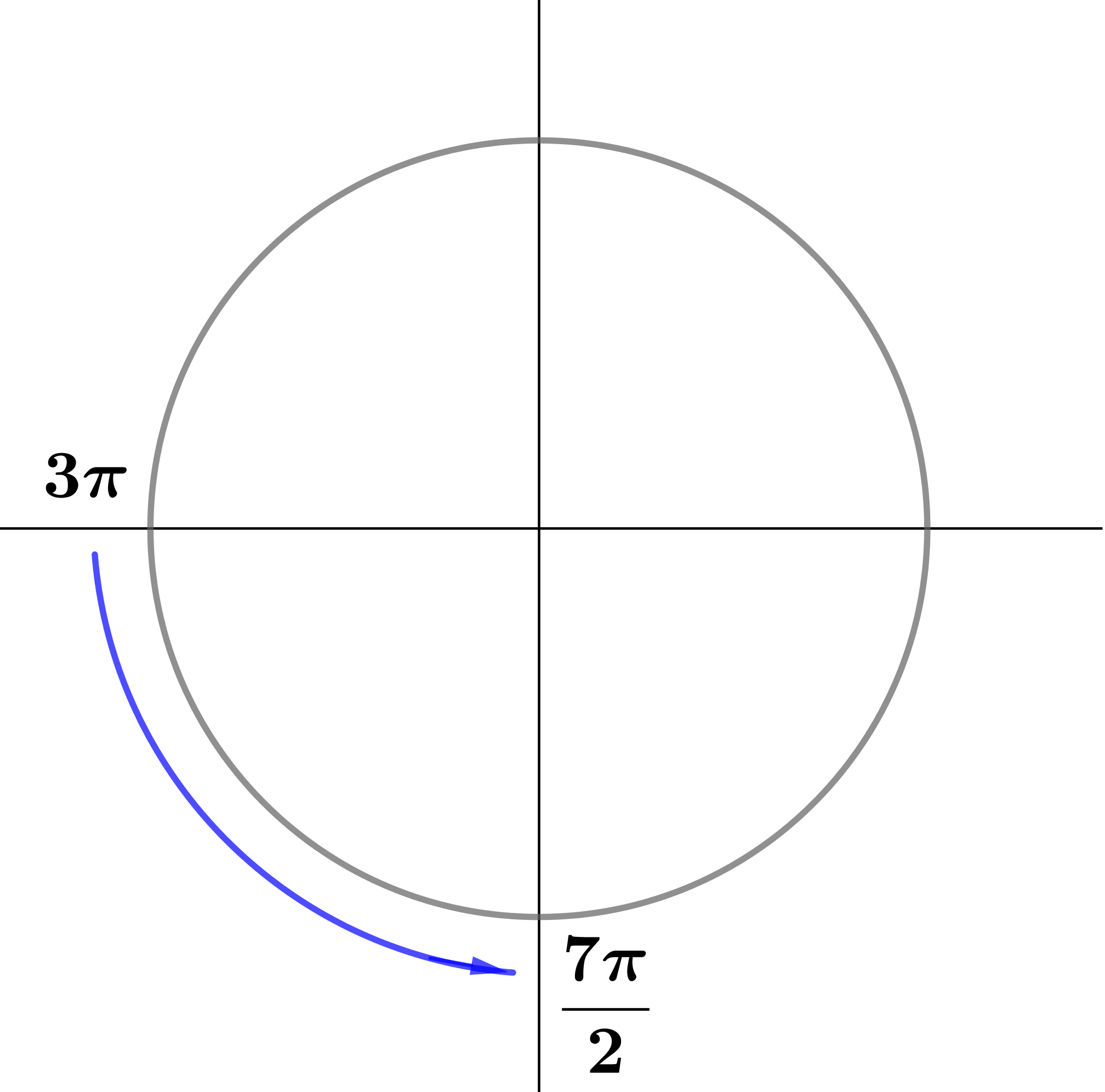
Определим, в какой четверти находится угол \(\displaystyle \frac{7\pi}{2}+\alpha { \small ,} \) предполагая \(\displaystyle \alpha \in \left(0;\frac{\pi}{2}\right){\small .}\)
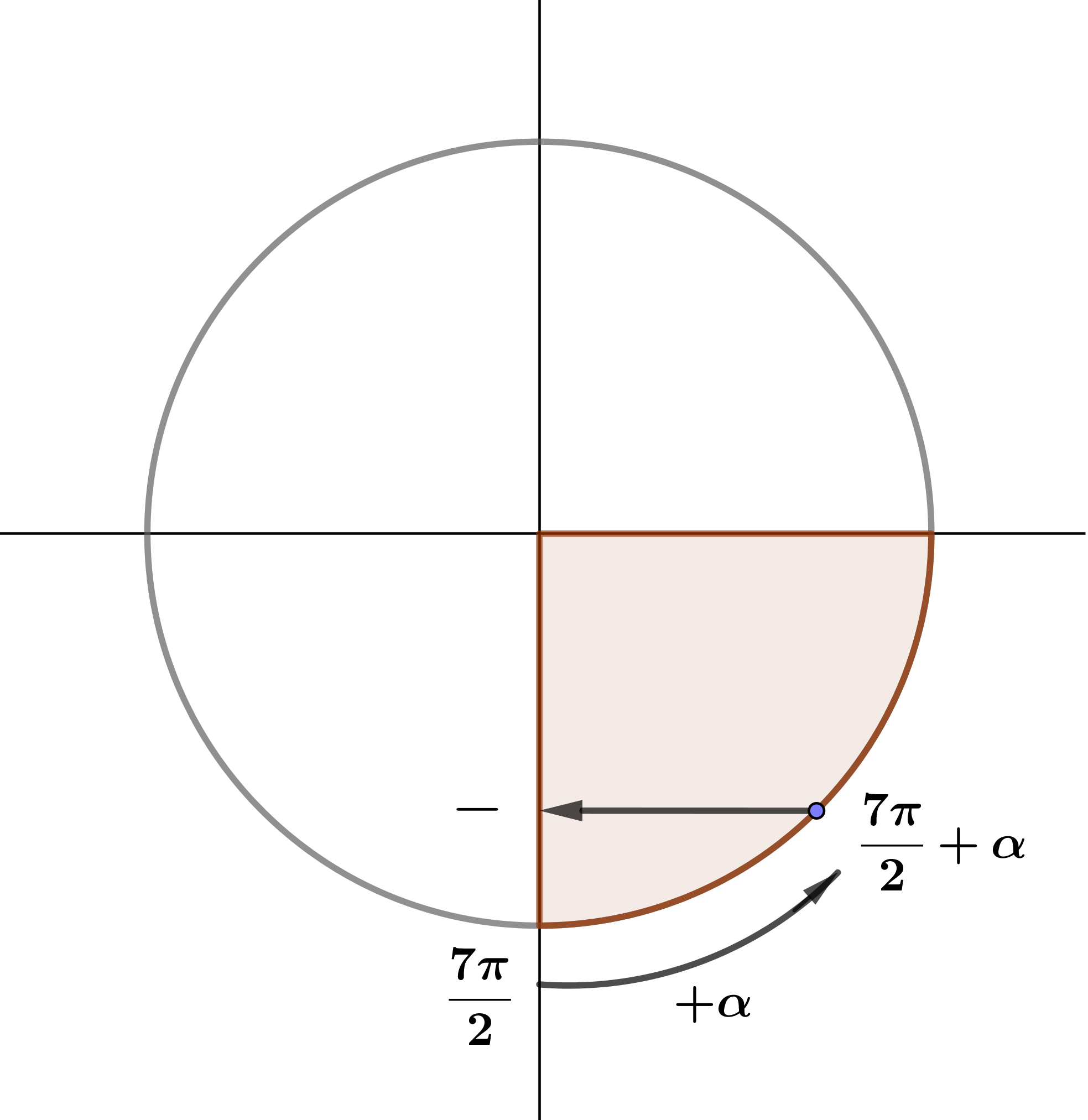
Значит, угол \(\displaystyle \frac{7\pi}{2}+\alpha \) находится в четвертой четверти.
2. Определим знак исходной функции.
В четвертой четверти синус отрицательный (\(\displaystyle {\bf -}\)).
3. Определим, какая будет функция.
Так как к аргументу \(\displaystyle \alpha\) прибавляем \(\displaystyle \frac{7\pi}{2}\) (нечетное число половинок \(\displaystyle \pi\)), то функция меняется.
Значит,
\(\displaystyle \sin \bigg(\frac{7\pi}{2}+\alpha \bigg)=-\cos \alpha {\small .}\)
Подставляем заданное значение \(\displaystyle \cos \alpha = 0{,}2 :\)
\(\displaystyle -\cos \alpha = -0{,}2{\small .}\)
Таким образом, верна следующая цепочка равенств:
\(\displaystyle \sin (\alpha +\frac{7\pi}{2})=\sin (\frac{7\pi}{2}+\alpha )= -\cos \alpha = -0{,}2{\small .}\)
Ответ: \(\displaystyle -0{,}2 {\small.} \)