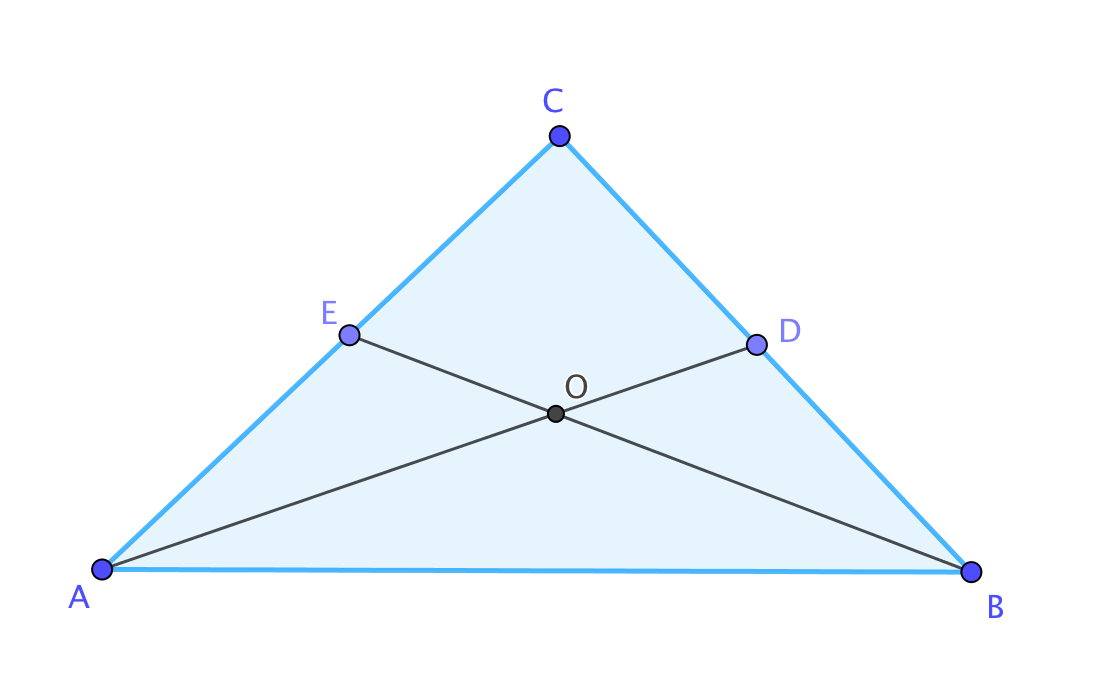
В треугольнике \(\displaystyle ABC\) \(\displaystyle \angle C=58^{\circ}{\small , }\) \(\displaystyle AD\) и \(\displaystyle BE\) – биссектрисы, пересекающиеся в точке \(\displaystyle O{\small .}\)
Найдите угол \(\displaystyle AOB{\small .}\)
\(\displaystyle \angle AOB=\)\(\displaystyle ^{\circ}\)
Пусть \(\displaystyle \angle A=x{\small , } \) а \(\displaystyle \angle B=y{\small .} \) Так как сумма углов в треугольнике равна \(\displaystyle 180^\circ{\small , } \) то
\(\displaystyle \angle A+ \angle B+ \angle C= 180^\circ{\small , } \)
то есть \(\displaystyle x+y+58^\circ= 180^\circ{\small .} \)
Угол \(\displaystyle OAB \) равен половине угла \(\displaystyle A{\small , } \) то есть \(\displaystyle \angle OAB= \frac{ x}{ 2}{\small .} \)
Угол \(\displaystyle OBA \) равен половине угла \(\displaystyle B{\small , } \) то есть \(\displaystyle \angle OBA= \frac{ y}{ 2}{\small .} \)
Тогда
\(\displaystyle x+y= 180^\circ-58^\circ{\small ,} \)
\(\displaystyle x+y= 122^\circ, \)
и, значит, \(\displaystyle \frac{ x}{ 2}+ \frac{y}{2}= 61^\circ{\small . } \)
Искомый угол \(\displaystyle AOB: \)
\(\displaystyle \angle OAB+ \angle OBA+ \angle AOB= 180^\circ{\small , } \)
\(\displaystyle \frac{ x}{ 2}+ \frac{y}{2}+\angle AOB= 180^\circ{\small , } \)
\(\displaystyle 61^\circ+ \angle AOB= 180^\circ{\small , } \)
\(\displaystyle \angle AOB= 180^\circ- 61^\circ= 119^\circ{\small . } \)
Ответ: \(\displaystyle 119^\circ{\small . } \)