В треугольнике \(\displaystyle ABC\) угол \(\displaystyle \angle A\) равен \(\displaystyle 40^{\circ}{\small , }\) внешний угол при вершине \(\displaystyle B\) равен \(\displaystyle 102^{\circ}.\) Найдите угол \(\displaystyle C{\small .}\)
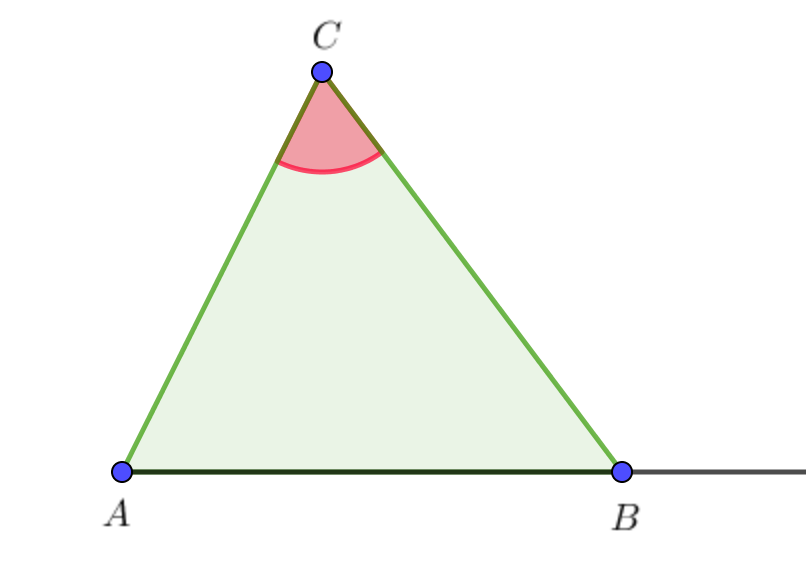
\(\displaystyle \angle C=\)\(\displaystyle ^{\circ}\)
Так как внешний угол при вершине равен сумме внутренних углов, не смежных с ним, то \(\displaystyle \angle A+ \angle C=102^{\circ}{\small .} \) Значит,
\(\displaystyle 40+ \angle C=102{\small , } \)
\(\displaystyle \angle C=102-40{\small , } \)
\(\displaystyle \angle C=62{\small .} \)
Ответ: \(\displaystyle 62^{\circ}{\small .} \)