В треугольнике \(\displaystyle ABC\) угол \(\displaystyle C\) равен \(\displaystyle 90^{\circ}{\small , }\) \(\displaystyle AB=4\sqrt{15}\) и \(\displaystyle \cos(A)=0{,}25{\small .}\)
Найдите высоту \(\displaystyle CH{\small .}\)
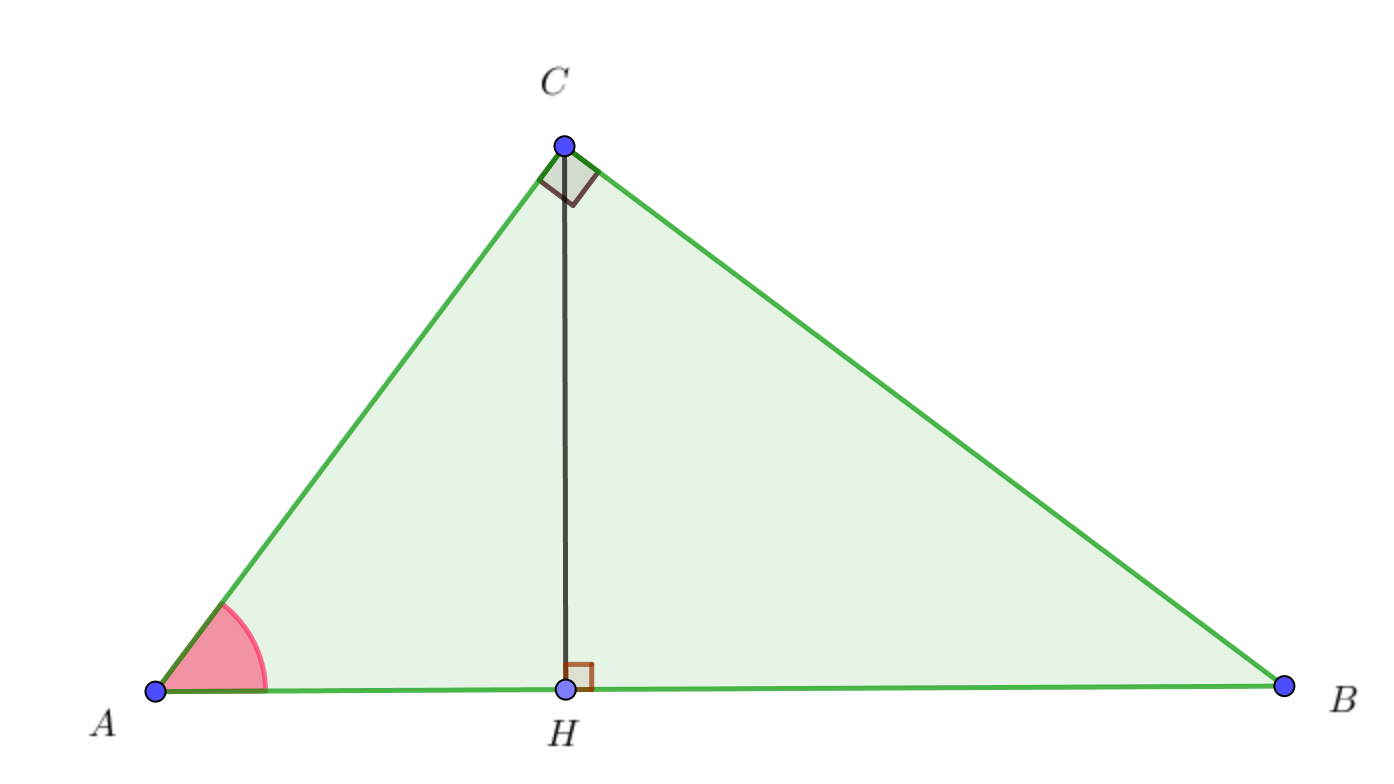
По определению косинуса в прямоугольном треугольнике \(\displaystyle \cos(A)=\frac{AC}{AB}{\small .}\) Тогда \(\displaystyle AC=AB \cdot \cos(A){\small .}\) | 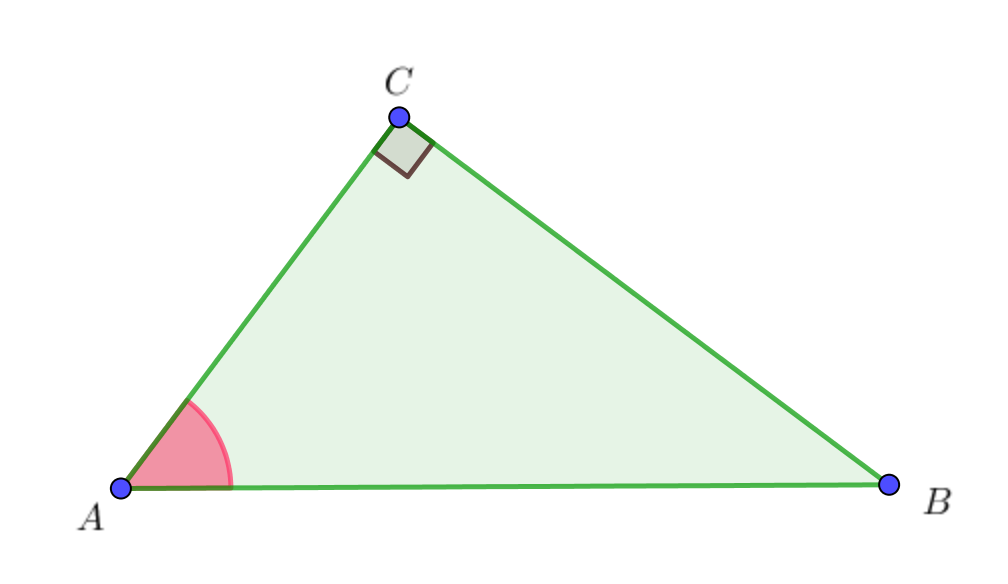 |
Так как \(\displaystyle AB=4\sqrt{15}\) и \(\displaystyle \cos(A)=0{,}25{\small , }\) то
\(\displaystyle AC= 4\sqrt{15}\cdot 0{,}25=\sqrt{15}{\small .}\\ \)
По теореме Пифагора
\(\displaystyle AB^2=AC^2+CB^2{\small , }\)
\(\displaystyle (4\sqrt{15})^2=(\sqrt{15})^2+CB^2{\small .}\)
\(\displaystyle CB^2=(4\sqrt{15})^2-(\sqrt{15})^2{\small , }\)
\(\displaystyle CB^2=16\cdot 15-15=15 \cdot 15=15^2{\small . }\)
Так как длина отрезка не может быть отрицательной, то \(\displaystyle CB=15{\small .}\)
Вычислим площадь треугольника \(\displaystyle ABC\) двумя способами:

- Половина произведения катетов \(\displaystyle AC\) и \(\displaystyle CB{\small:} \)
\(\displaystyle S_{ABC}=\frac{1}{2}\cdot AC\cdot BC=\frac{1}{2}\cdot \sqrt{15}\cdot 15=\frac{15 \cdot \sqrt{15}}{2}{\small .}\\ \)
- Половина произведения основания \(\displaystyle AB\) на высоту \(\displaystyle CH{\small:}\\ \)\(\displaystyle S_{ABC}=\frac{1}{2} CH \cdot AB= \frac{1}{2} CH \cdot 4\sqrt{15}=CH \cdot 2\sqrt{15}{\small .}\)
Приравнивая, получаем:
\(\displaystyle \frac{15 \cdot \sqrt{15}}{2}=CH \cdot 2\sqrt{15}{\small , }\)
\(\displaystyle CH=\frac{15\cdot \cancel{\sqrt{15}}}{4\cdot \cancel{\sqrt{15}}}{\small , }\)
\(\displaystyle CH=\frac{15}{4}=3{,}75{\small .}\)
Ответ: \(\displaystyle 3{,}75 {\small .}\)