Одна сторона прямоугольного треугольника, вписанного в окружность, равна \(\displaystyle \sqrt{2}{\small . }\) Радиус описанной окружности равен \(\displaystyle 1{\small . }\) Найдите острый угол, противолежащий данной стороне (ответ дайте в градусах).
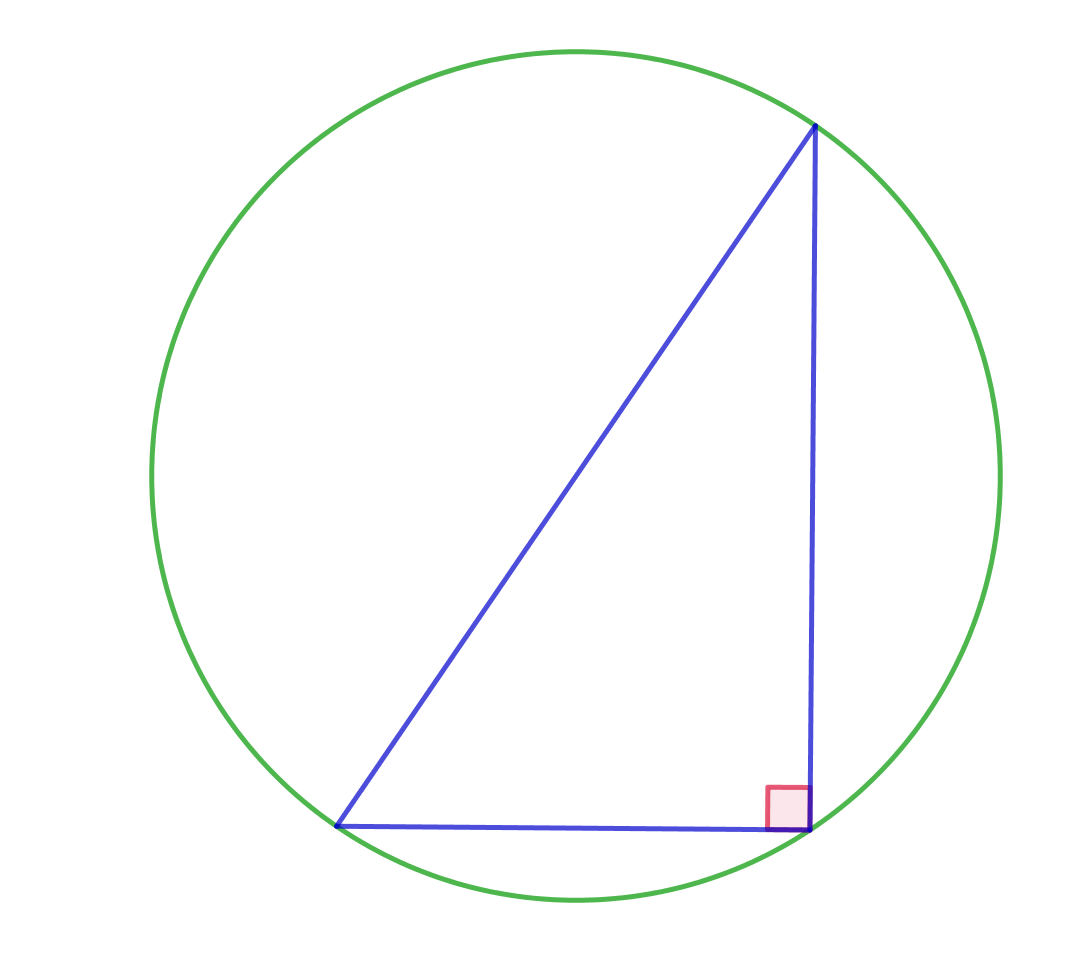
Описанная окружность и прямоугольный треугольник
Центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы, а её радиус равен половине гипотенузы.
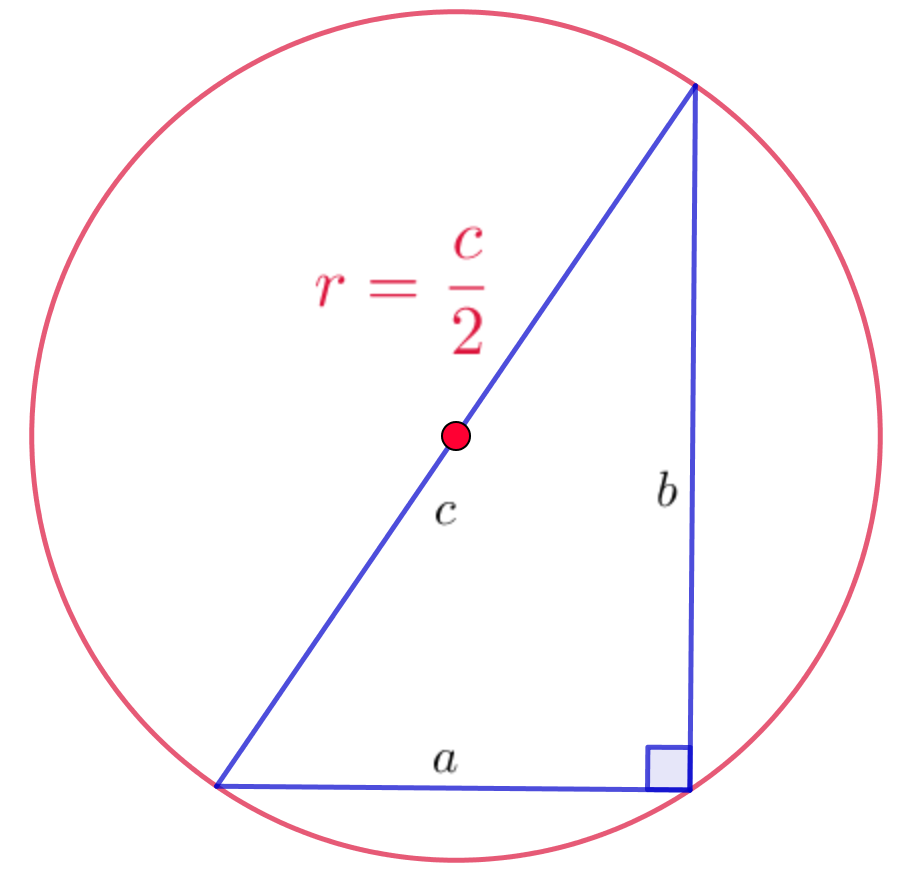
Так как радиус описанной окружности равен \(\displaystyle r=1{\small , }\) то гипотенуза прямоугольного треугольника равна
\(\displaystyle c=2 \cdot r=2\cdot 1=2{\small .}\)
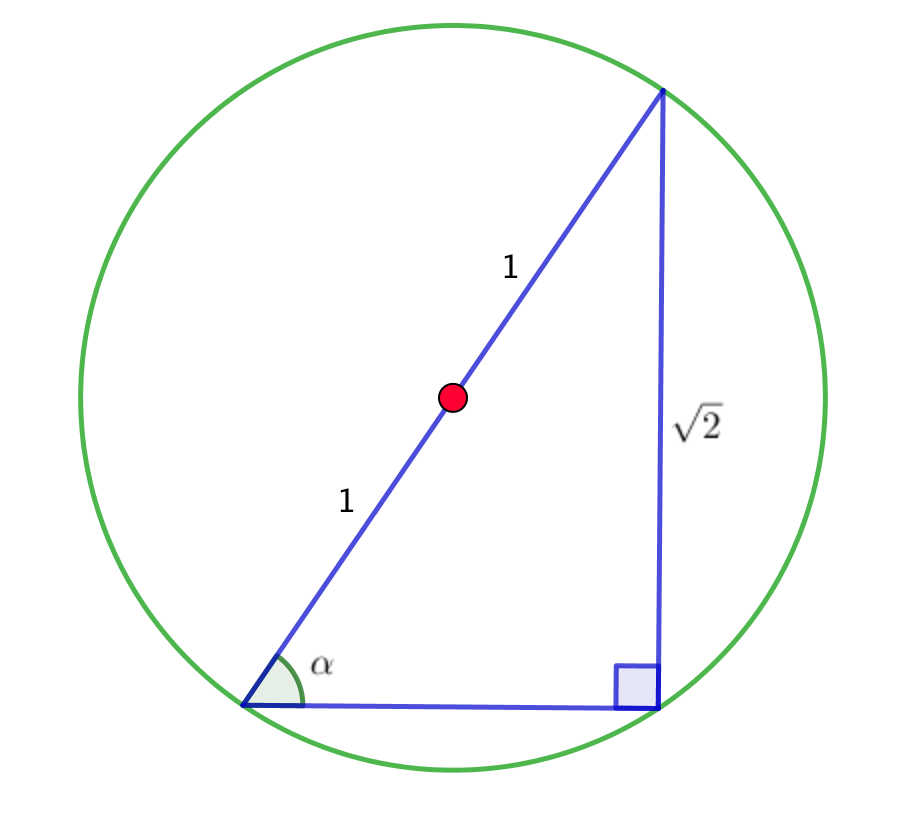
Пусть \(\displaystyle \alpha \) – угол, лежащий напротив катета длиной \(\displaystyle \sqrt{2}{\small.}\)
Синус угла в прямоугольном треугольнике – это отношение противолежащего катета к гипотенузе.
Следовательно,
\(\displaystyle \sin\alpha=\frac{\sqrt{2}}{2}{\small .}\)
Согласно таблице значений синуса \(\displaystyle \sin45^{\circ}=\frac{\sqrt{2}}{2}{\small . }\) Значит,
\(\displaystyle \alpha=45^{\circ}{\small .}\)
Ответ: \(\displaystyle 45^{\circ}{\small .}\)