Синус острого угла \(\displaystyle A\) треугольника \(\displaystyle ABC\) равен \(\displaystyle \frac{3 \sqrt{11}}{10} {\small.}\) Найдите \(\displaystyle \cos \angle A {\small.}\)
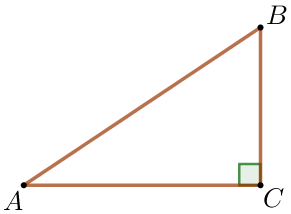
В прямоугольном треугольнике синус и косинус острого угла \(\displaystyle A\) связаны соотношением
\(\displaystyle \sin ^2 \angle A +\cos ^2 \angle A =1{\small.}\)
По условию \(\displaystyle \sin \angle A = \frac{3 \sqrt{11}}{10} {\small.}\) Тогда
\(\displaystyle \left( \frac{3 \sqrt{11}}{10} \right) ^2 +\cos ^2 \angle A =1{\small.}\)
Следовательно,
\(\displaystyle \cos ^2 \angle A =1- \left( \frac{3 \sqrt{11}}{10} \right) ^2 = 1 - \frac {99}{100}=\frac{1}{100}{\small.}\)
Так как в прямоугольном треугольнике косинус острого угла положителен, то
\(\displaystyle \cos \angle A =\sqrt{\frac{1}{100}}=\frac{1}{10}=0{,}1{\small.}\)
Ответ: \(\displaystyle 0{,}1{\small.}\)