Установите соответствие функциями и их графиками.
| \(\displaystyle y=-2x^2+13x-22\) | \(\displaystyle y=2x^2-13x+22\) | \(\displaystyle y=2x^2+13x+22\) |
Проще искать соответствие между графиками квадратичных функций (параболами) и формулами, которые их задают.
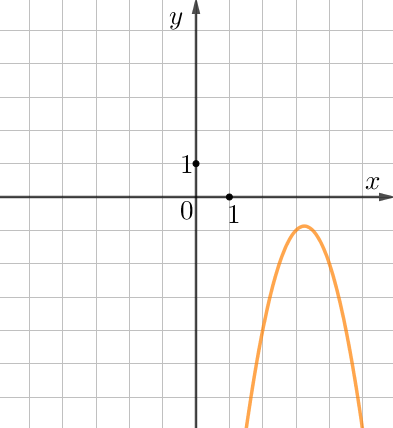
1. Заметим, что только у оранжевой параболы ветви направлены вниз.
Значит, только в уравнении этой параболы коэффициент при \(\displaystyle x^2\) отрицателен.
Среди представленных уравнений уравнение с отрицательным старшим коэффициентом единственное – это \(\displaystyle y=\color{magenta}{-2} \cdot x^2+13x-22{\small.}\)
Поэтому оранжевая парабола задана уравнением \(\displaystyle y=-2x^2+13x-22{\small.}\)
2. Соответствие между двумя оставшимися параболами и уравнениями установим по знакам абсцисс вершин.
1. Найдём знаки абсцисс вершин по графикам:
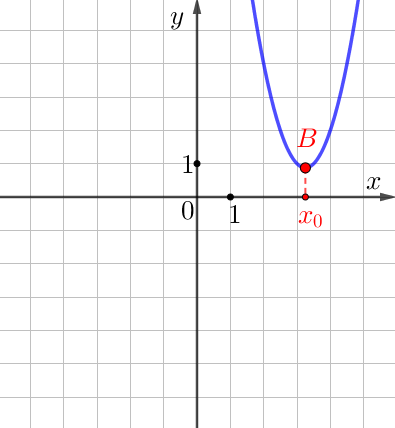 | 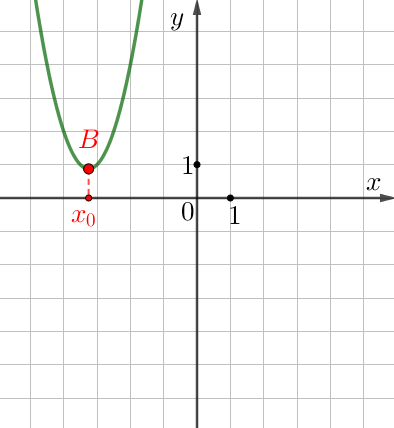 |
| абсцисса вершины положительна | абсцисса вершины отрицательна |
2. Найдём знаки абсцисс вершин парабол \(\displaystyle y=2x^2+13x+22{\small}\) и \(\displaystyle y=2x^2-13x+22{\small.}\)
3. Сопоставим результаты и сделаем выводы.
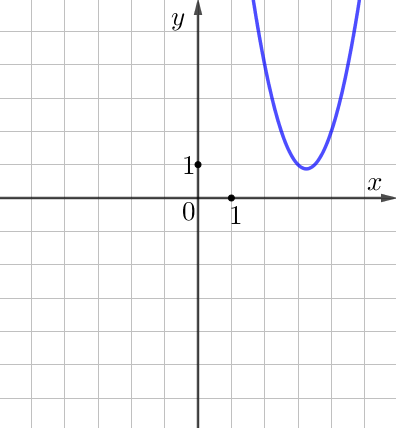
- У синей параболы и параболы \(\displaystyle y=2x^2-13x+22\) абсциссы вершин положительны.
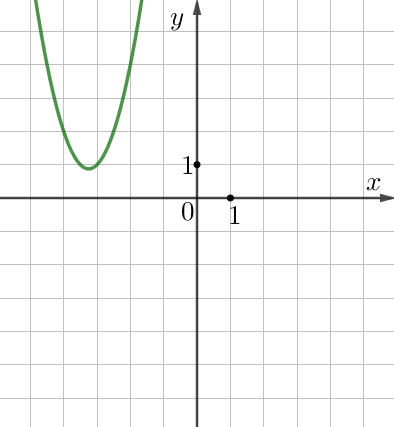
То есть синяя парабола задана уравнением \(\displaystyle y=2x^2-13x+22{\small .}\) - У зелёной параболы и параболы \(\displaystyle y=2x^2+13x+22{\small}\) абсциссы вершин отрицательны,
То есть зелёная парабола задана уравнением \(\displaystyle y=2x^2+13x+22{\small .}\)
3. Окончательно получаем соответствие:
| \(\displaystyle y=-2x^2+13x-22\) | \(\displaystyle y=2x^2-13x+22\) | \(\displaystyle y=2x^2+13x+22\) |
 |  |  |