Skip to main content

Теория: 08 Положение графика квадратичной функции \(\displaystyle y=ax^2+bx+c\) и вершина параболы

Задание

На рисунке изображен график функции \(\displaystyle f(x)=-2x^2+x+2{\small.}\) Точка \(\displaystyle B\) – вершина параболы. Найдите её абсциссу \(\displaystyle x_0{\small.}\)

 

 

\(\displaystyle x_0=\)
0,25
Решение

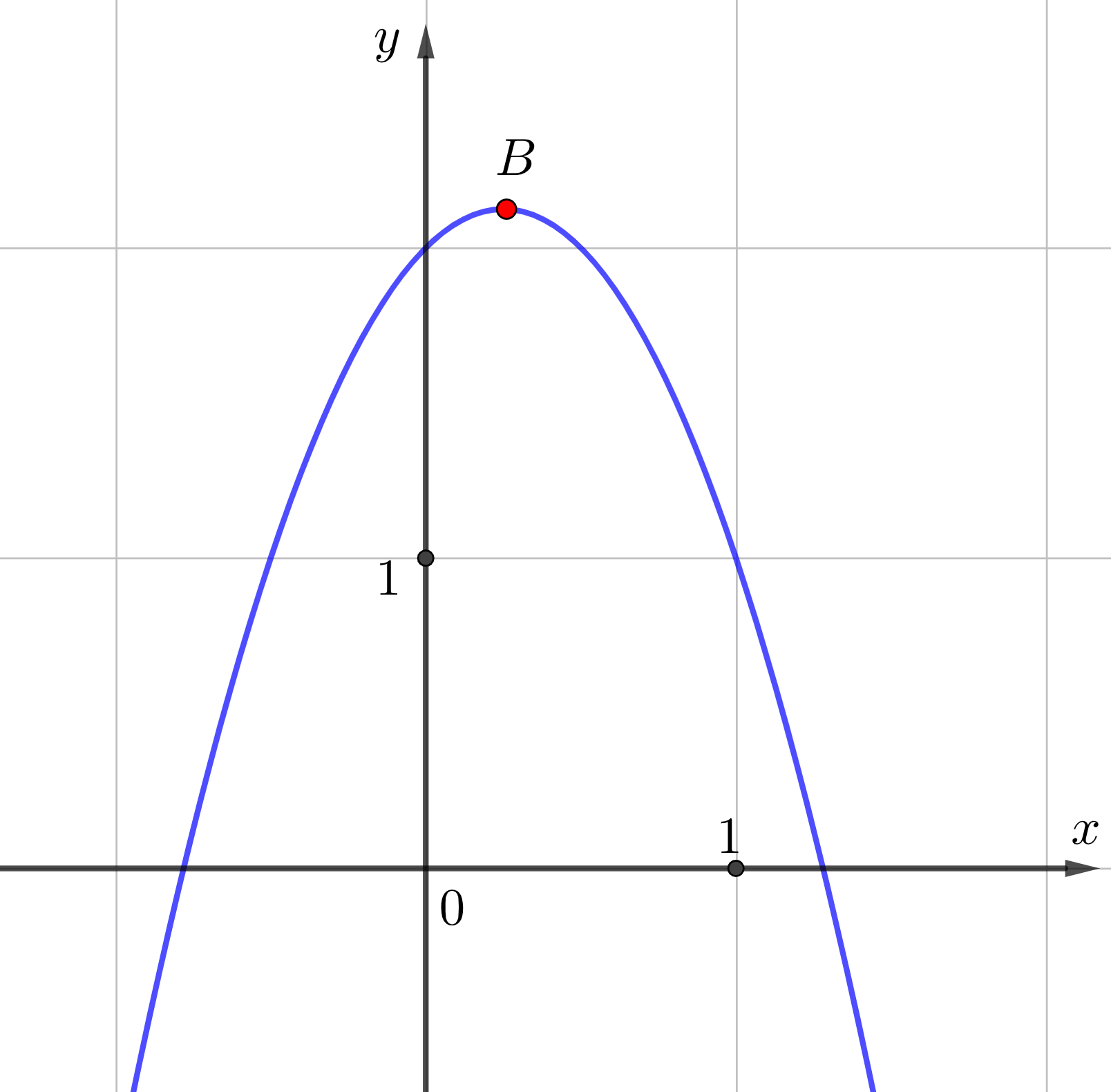
Найдём абсциссу \(\displaystyle {x_0}\) вершины параболы по формуле:

Правило

Абсцисса вершины параболы

Абсцисса \(\displaystyle x_0\) вершины параболы \(\displaystyle y=\color{red}ax^2+\color{blue}bx+\color{green}c\) находится по формуле: 

\(\displaystyle x_0=\frac{-\color{blue}b}{2\color{red}a}{\small.}\)

У нас 

\(\displaystyle y=\color{red}{-2}x^2+{\color{blue}{1}}x+\color{green}{2}{\small.}\) 

Тогда 

\(\displaystyle {x_0}=\frac{-\color{blue}{1}}{2\cdot(\color{red}{-2})}{\small,}\)
 

\(\displaystyle {x_0}=\frac{{-1}}{-4}=0{,}25{\small.}\)

 

Ответ: \(\displaystyle 0{,}25{\small.}\)