В кубе \(\displaystyle ABCDA_1B_1C_1D_1\) отмечены середины \(\displaystyle M\) и \(\displaystyle N\) отрезков \(\displaystyle AB\) и \(\displaystyle AD\) соответственно.
\(\displaystyle а)\) Докажите, что прямые \(\displaystyle B_1N\) и \(\displaystyle CM\) перпендикулярны.
\(\displaystyle б)\) Найдите расстояние между этими прямыми, если \(\displaystyle B_1N=3\sqrt{5}{\small.}\)
По условию задачи выполним чертёж.
\(\displaystyle ABCDA_1B_1C_1D_1\) – куб, точка \(\displaystyle M\) – середина отрезка \(\displaystyle AB{\small,}\) точка \(\displaystyle N\) – середина отрезка \(\displaystyle AD{\small,}\) \(\displaystyle B_1N\) и \(\displaystyle CM\) – прямые. |
\(\displaystyle а)\) Требуется доказать, что прямые \(\displaystyle B_1N\) и \(\displaystyle CM\) перпендикулярны.
Воспользуемся теоремой о трёх перпендикулярах:
Теорема о трёх перпендикулярах
Прямая \(\displaystyle l{\small,}\) проведенная в плоскости через основание наклонной перпендикулярно к её проекции на эту плоскость, перпендикулярна и к самой наклонной. \(\displaystyle l\perp BH\) \(\displaystyle \Rightarrow\) \(\displaystyle l \perp AB{\small,}\) где \(\displaystyle AB\) – наклонная к плоскости \(\displaystyle \alpha{\small,}\) \(\displaystyle BH\) – проекция наклонной \(\displaystyle AB\) на плоскость \(\displaystyle \alpha{\small.}\) | 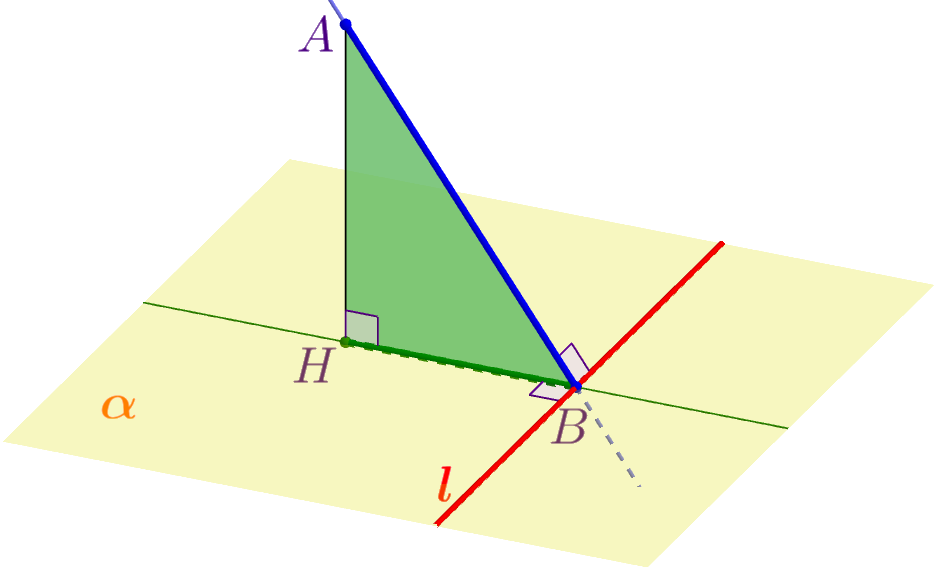 |
\(\displaystyle CM\) – лежит в плоскости \(\displaystyle ABC{\small,}\) \(\displaystyle B_1N\) – наклонная к плоскости \(\displaystyle ABC{\small,}\) \(\displaystyle BN\) – проекция \(\displaystyle B_1N\) на плоскость \(\displaystyle ABC{\small.}\) |
Докажем, что \(\displaystyle BN \perp CM{\small.}\)
Рассмотрим прямоугольные треугольники \(\displaystyle CBM\) и \(\displaystyle BAN{\small.}\)
Следовательно, \(\displaystyle \triangle CBM =\triangle BAN {\small.}\) (прямоугольные треугольники равны по двум катетам) Тогда \(\displaystyle \angle BCM= \angle ABN = \color{red}{\alpha} {\small,}\) \(\displaystyle \angle BMC= \angle ANB= \color{blue}{\beta} {\small.}\) |
Так как в прямоугольном треугольнике сумма острых углов равна \(\displaystyle 90^{\circ}{\small,}\) то \(\displaystyle \color{red}{\alpha} + \color{blue}{\beta} = 90^{\circ}{\small.} \)
Пусть \(\displaystyle O\) – точка пересечения отрезков \(\displaystyle BN\) и \(\displaystyle CM{\small.}\)
Рассмотрим треугольник \(\displaystyle BOM{\small:}\)
Тогда \(\displaystyle \angle BOM= 180^{\circ}-(\color{red}{\alpha}+\color{blue}{\beta}) {\small,}\) \(\displaystyle \angle BOM= 180^{\circ}-90^{\circ}=90^{\circ}{\small.}\)
|
Значит,
\(\displaystyle BN \perp CM{\small.}\)
Следовательно, по теореме о трёх перпендикулярах
\(\displaystyle B_1N \perp CM{\small.}\)
Что и требовалось доказать.
\(\displaystyle б)\) Требуется найти расстояние между прямыми \(\displaystyle B_1N\) и \(\displaystyle CM{\small,}\) если \(\displaystyle B_1N=3\sqrt{5}{\small.}\)
Прямые \(\displaystyle B_1N\) и \(\displaystyle CM\) являются скрещивающимися.
Расстояние между двумя скрещивающимися прямыми равно длине отрезка их общего перпендикуляра.
Построим общий перпендикуляр к прямым \(\displaystyle CM\) и \(\displaystyle B_1N{\small.}\)
По доказанному ранее известно, что \(\displaystyle CM \perp BN \) и \(\displaystyle CM \perp B_1N {\small.}\)
Так как \(\displaystyle CM\) перпендикулярна двум пересекающимся прямым, лежащим в плоскости \(\displaystyle BNB_1{\small,}\) то по признаку перпендикулярности прямой и плоскости прямая \(\displaystyle CM\) перпендикулярна плоскости \(\displaystyle BNB_1{\small.}\) Значит, \(\displaystyle CM\) перпендикулярна любой прямой, лежащей в этой плоскости. |
Прямая \(\displaystyle B_1N\) лежит в плоскости \(\displaystyle BNB_1{\small,}\) прямая \(\displaystyle CM\) пересекает плоскость \(\displaystyle BNB_1\) в точке \(\displaystyle O{\small.}\)
В плоскости \(\displaystyle BNB_1\) из точки \(\displaystyle O\) к прямой \(\displaystyle B_1N\) построим перпендикуляр \(\displaystyle OH{\small.}\)
\(\displaystyle OH\)– отрезок общего перпендикуляра к прямым \(\displaystyle CM\) и \(\displaystyle B_1N{\small.}\) Его длина равна расстоянию между данными прямыми. |
Сначала найдем длину ребра куба.
Найдем длину отрезка \(\displaystyle OH{\small.}\)
В прямоугольном треугольнике \(\displaystyle OHN\) \(\displaystyle \frac{OH}{ON}= \sin \angle ONH {\small.}\) Тогда \(\displaystyle OH=ON \cdot \sin \angle ONH {\small.}\) |
Получаем
\(\displaystyle OH=ON \cdot \sin \angle ONH =3 \cdot \frac{2}{3}=2{\small.}\)
Ответ: \(\displaystyle б)\) \(\displaystyle 2{\small.}\)