На рисунках изображены графики функций вида \(\displaystyle y=kx+b \small.\)
Установите соответствие между знаками коэффициента \(\displaystyle \small\) и графиками функций.
| \(\displaystyle k>0 \) | \(\displaystyle k=0 \) | \(\displaystyle k<0 \) |
Даны три прямые – графики линейных функций \(\displaystyle y=kx+b \small.\)
Нужно установить соответствие между знаками \(\displaystyle k\) и данными графиками.
Удобнее установить соответствие между графиками и знаками \(\displaystyle k \small.\)
Определим для каждой прямой знак коэффициента \(\displaystyle k \small.\)
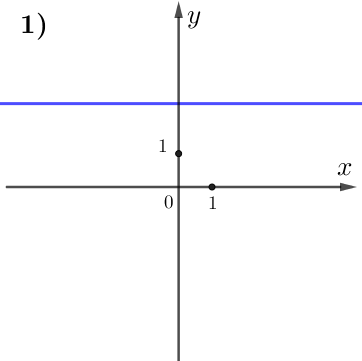
По графику видим:
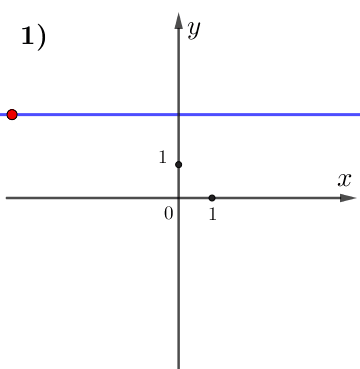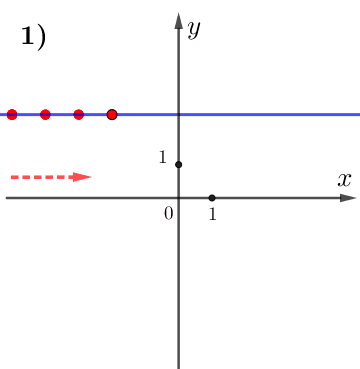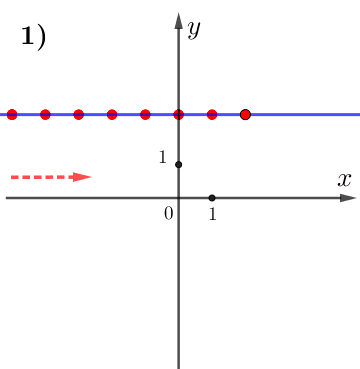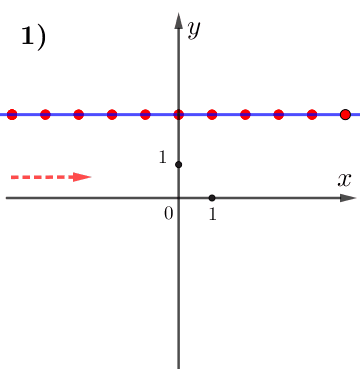
при увеличении значения \(\displaystyle x\) значение \(\displaystyle y\) не изменяется.
Поэтому данная функция постоянна, а, значит,
\(\displaystyle k=0 {\small . }\)
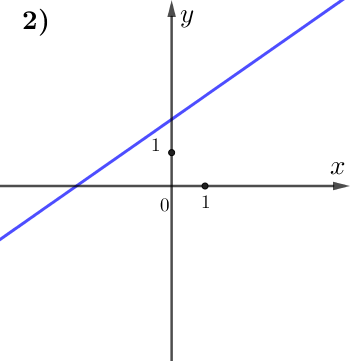
По графику видим:
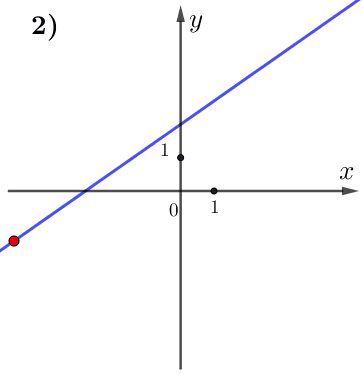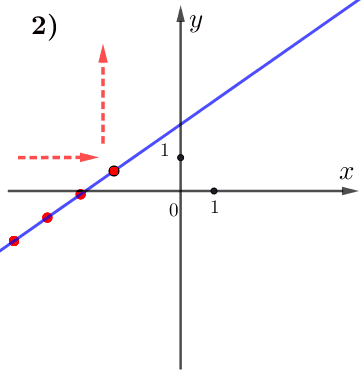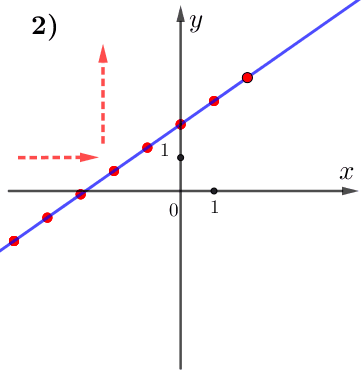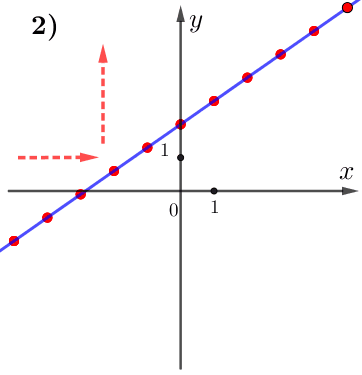
при увеличении значения \(\displaystyle x\) значение \(\displaystyle y\) тоже увеличивается.
Поэтому данная функция возрастает, а, значит,
\(\displaystyle k>0 {\small . }\)
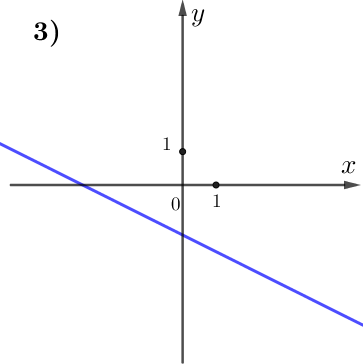
По графику видим:
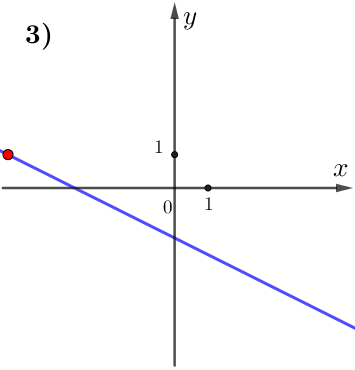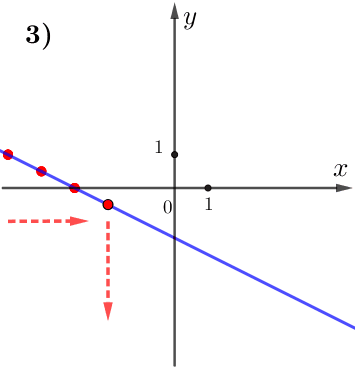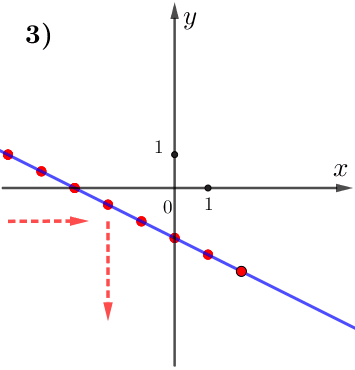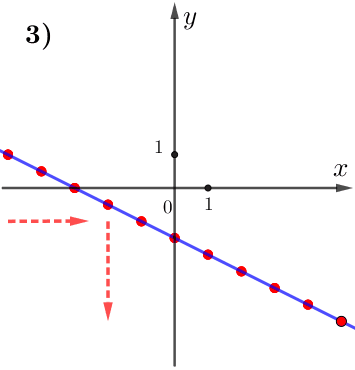
при увеличении значения \(\displaystyle x\) значение \(\displaystyle y\) уменьшается.
Поэтому данная функция убывает, а, значит,
\(\displaystyle k<0 {\small . }\)
Запишем ответ:
| \(\displaystyle k>0 \) | \(\displaystyle k=0 \) | \(\displaystyle k<0 \) |
 |  |  |