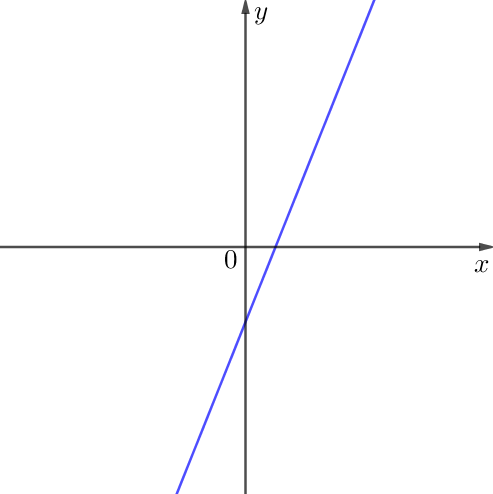
На рисунке изображён график функции вида \(\displaystyle y=kx+b \small.\) Определите знак коэффициента \(\displaystyle b \small.\)
\(\displaystyle b\) \(\displaystyle 0 \small.\)
Функция вида \(\displaystyle y=kx+b \small\) – линейная. На рисунке изображён её график – прямая.
Требуется определить знак коэффициента \(\displaystyle b \small.\)
Напомним, что \(\displaystyle \color {red}b\) – это ордината точки пересечения прямой \(\displaystyle y=kx+b \small\) с осью \(\displaystyle Oy{\small .}\)
Отметим точку пересечения данной прямой с осью \(\displaystyle Oy{\small . }\)
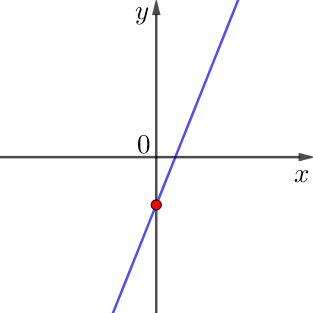
Эта точка находится ниже оси \(\displaystyle Ox{\small , }\) поэтому её ордината \(\displaystyle \color {red} {b}\) отрицательна.
То есть
\(\displaystyle \color {red} {b}<0 {\small . }\)
Ответ: \(\displaystyle b<0 {\small . }\)