В треугольнике \(\displaystyle ABC\) биссектриса угла \(\displaystyle A\) делит высоту, проведённую из вершины \(\displaystyle B\) в отношении \(\displaystyle 17:15 {\small,}\) считая от точки \(\displaystyle B {\small.}\) Найдите длину стороны \(\displaystyle BC {\small,}\) если радиус окружности, описанной около треугольника \(\displaystyle ABC {\small,}\) равен \(\displaystyle 17 {\small.}\)
Ознакомьтесь с решением аналогичной задачи:
В треугольнике \(\displaystyle ABC\) биссектриса угла \(\displaystyle A\) делит высоту, проведённую из вершины \(\displaystyle B\) в отношении \(\displaystyle 5:3 {\small,}\) считая от точки \(\displaystyle B {\small.}\) Найдите длину стороны \(\displaystyle BC {\small,}\) если радиус окружности, описанной около треугольника \(\displaystyle ABC {\small,}\) равен \(\displaystyle 5 {\small.}\)
Решение.
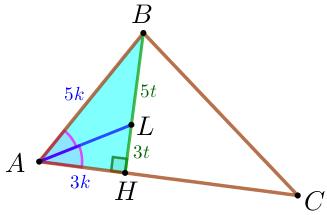
Выполним чертёж по условию задачи.
 | Пусть в треугольнике \(\displaystyle ABC{\small:}\)
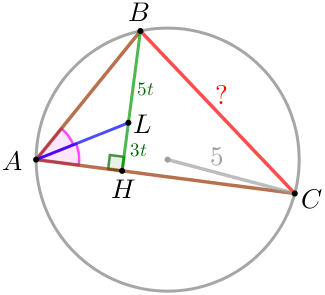
По условию \(\displaystyle \frac{BL}{LH}=\frac{5}{3} {\small,}\) \(\displaystyle R=5 \) – радиус окружности, описанной около треугольника \(\displaystyle ABC{\small.}\) Требуется найти длину стороны \(\displaystyle BC {\small.}\) |
\(\displaystyle \frac{BC}{\sin \angle A}=2 \cdot R {\small,}\\ \)
\(\displaystyle BC=2 \cdot R \cdot \sin \angle A {\small,}\\ \)
\(\displaystyle BC=2 \cdot 5 \cdot \sin \angle A =10 \cdot \sin \angle A{\small.}\\ \)
Нужно найти \(\displaystyle \sin \angle A{\small.}\)
Рассмотрим прямоугольный треугольник \(\displaystyle ABH{\small:}\)
|
|
\(\displaystyle \frac{AH}{AB}=\frac{LH}{BL}=\frac{3}{5} {\small.}\)
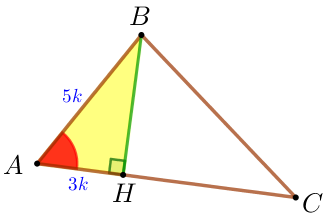 | Поскольку для острого угла в прямоугольном треугольнике отношение прилежащего катета к гипотенузе равно косинусу этого угла, то \(\displaystyle \cos \angle A = \frac{AH}{AB}=\frac{3}{5} {\small.}\) По основному тригонометрическому тождеству: \(\displaystyle (\sin \angle A)^2+(\cos \angle A)^2=1{\small.}\) |
Тогда
\(\displaystyle (\sin \angle A)^2=1-(\cos \angle A)^2=1- \bigg(\frac{3}{5}\bigg)^2=1-\frac{9}{25}=\frac{25-9}{25}=\frac{16}{25}= \bigg(\frac{4}{5}\bigg)^2{\small.}\\ \)
Значит, \(\displaystyle \sin \angle A= \frac{4}{5} {\small.}\)
Получаем
\(\displaystyle BC=10 \cdot \sin \angle A=10 \cdot \frac{4}{5}=8{\small.} \)
Ответ: \(\displaystyle 8 {\small.}\)