Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся, как \(\displaystyle 6:7:23 {\small.}\) Найдите меньший угол треугольника.
Пусть \(\displaystyle ABC\) – треугольник, вписанный в окружность. При этом
\(\displaystyle \overset{\smile}{AB}:\overset{\smile}{BC}:\overset{\smile}{AC}=6:7:23 {\small.} \)
Найдём градусные меры дуг, на которые вершины треугольника делят описанную около него окружность.
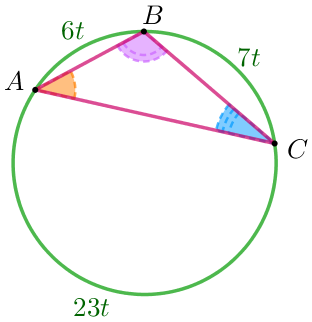 | Обозначим \(\displaystyle \overset{\smile}{AB}=6t {\small,}\) \(\displaystyle \overset{\smile}{BC}=7t {\small,}\) \(\displaystyle \overset{\smile}{AC}=23t {\small.}\) Поскольку градусная мера окружности равна \(\displaystyle 360^{\circ} {\small,}\) то \(\displaystyle \overset{\smile}{AB}+\overset{\smile}{BC}+\overset{\smile}{AC}=360^{\circ} {\small.} \) Получаем \(\displaystyle 6t+7t+23t=360^{\circ} {\small,}\) \(\displaystyle 36t=360^{\circ} {\small,}\) \(\displaystyle t=10^{\circ} {\small.}\) |
Следовательно,
\(\displaystyle \overset{\smile}{AB}=60^{\circ} {\small,}\) \(\displaystyle \overset{\smile}{BC}=70^{\circ} {\small,}\) \(\displaystyle \overset{\smile}{AC}=230^{\circ} {\small.}\)
Вписанный угол измеряется половиной дуги, на которую он опирается.
Найдём градусные меры углов треугольника \(\displaystyle ABC {\small:}\)
\(\displaystyle \angle A = \frac{1}{2}\cdot \overset{\smile}{BC}=\frac{1}{2} \cdot 70^{\circ} =35^{\circ}{\small,} \\ \)
\(\displaystyle \angle B = \frac{1}{2}\cdot \overset{\smile}{AC}=\frac{1}{2} \cdot 230^{\circ}=115^{\circ}{\small,} \\ \)
\(\displaystyle \angle C = \frac{1}{2}\cdot \overset{\smile}{AB}=\frac{1}{2} \cdot 60^{\circ} =30^{\circ}{\small.} \)
\(\displaystyle \angle C =30^{\circ}\) – меньший угол треугольника \(\displaystyle ABC{\small.}\)
Ответ: \(\displaystyle 30 {\small.}\)