Точка \(\displaystyle H\) является основанием высоты \(\displaystyle BH {\small,}\) проведённой из вершины прямого угла \(\displaystyle B\) прямоугольного треугольника \(\displaystyle ABC {\small.}\) Окружность с диаметром \(\displaystyle BH\) пересекает стороны \(\displaystyle AB\) и \(\displaystyle CB\) в точках \(\displaystyle P\) и \(\displaystyle K\) соответственно. Найдите \(\displaystyle BH {\small,}\) если \(\displaystyle PK=11 {\small.}\)
Выполним чертёж по условию задачи.
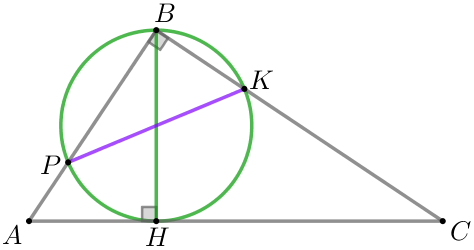 | В треугольнике \(\displaystyle ABC\) \(\displaystyle \angle B=90^{\circ} {\small,}\) \(\displaystyle BH\) – высота. По условию \(\displaystyle BH\) – диаметр окружности. Точки \(\displaystyle P\) и \(\displaystyle K\) лежат на окружности и \(\displaystyle PK=\color{darkviolet}{11} {\small.}\) |
По построенному чертежу:
- \(\displaystyle \angle PBK\) – вписан в окружность с диаметром \(\displaystyle BH {\small,}\)
- \(\displaystyle \angle PBK=90^{\circ}{\small.}\)
Величина вписанного угла
Величина вписанного угла равна половине дуги, на которую он опирается.
Значит,
\(\displaystyle \overset {\smile} {PHK}=2 \cdot \angle PBK=2 \cdot 90^{\circ}=180^{\circ} {\small.} \)
Следовательно, \(\displaystyle PK\) – диаметр окружности. То есть
\(\displaystyle BH=PK=11 {\small.}\)
Ответ: \(\displaystyle 11 {\small.}\)