Skip to main content

Теория: Линейная функция и её график

Задание

Установите соответствие между графиками функций и формулами, которые их задают:

\(\displaystyle А\)\(\displaystyle Б\)\(\displaystyle В\)
Перетащите сюда правильный ответ Перетащите сюда правильный ответ Перетащите сюда правильный ответ

 

Решение

Даны три прямые, которые являются графиками трёх данных линейных функций.

Требуется поставить в соответствие каждой прямой функцию, которая её задаёт.


Воспользуемся тем, что каждая прямая задана одним из трёх данных уравнений, и каждое из трёх уравнений задаёт только одну из данных прямых. 

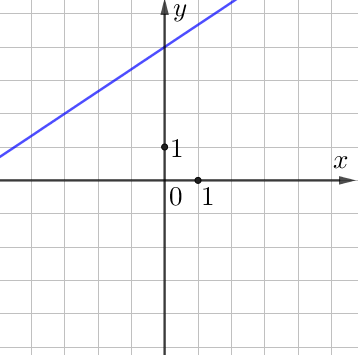
1. Сначала рассмотрим график \(\displaystyle А\small.\)

Выберем на нём точку, которая не лежит на двух других графиках, и найдём уравнение, которому удовлетворяет эта точка. Оно и будет определять график \(\displaystyle А\small.\)

Удобно взять на графике \(\displaystyle А\) точку с целочисленными координатами, назовём её \(\displaystyle M(\blue{-3};\,\color{blue}{2}){\small .}\) Она не лежит на двух других графиках.


Подставим координаты точки  \(\displaystyle M(\blue{-3};\,\color{blue}{2}{\small })\) в каждое из трёх уравнений.

Координаты точки \(\displaystyle M(-3;\,2)\) прямой \(\displaystyle А\) удовлетворяют уравнению \(\displaystyle y=\frac{2}{3}x+4{\small .}\)

Подставляя \(\displaystyle x=\blue{-3}\) и \(\displaystyle y=\color{blue}{2}\) в уравнение  \(\displaystyle y=\frac{2}{3}x+4{\small ,}\) получаем:

\(\displaystyle \color{blue}{2}=\frac{2}{3}\cdot (\blue {-3})+4{\small ;}\)
\(\displaystyle 2=2\) (верно)

Координаты точки \(\displaystyle M(-3;\,2)\) прямой \(\displaystyle А\) не удовлетворяют уравнению \(\displaystyle y=\frac{2}{3}x-4{\small .}\)

Координаты точки \(\displaystyle M(-3;\,2)\) прямой \(\displaystyle А\) не удовлетворяют уравнению \(\displaystyle y=-\frac{2}{3}x+4{\small .}\)

Следовательно, прямая \(\displaystyle А\) имеет уравнение \(\displaystyle y=\frac{2}{3}x+4{\small .}\) 

Исключим эту прямую и это уравнение из дальнейшего рассмотрения.


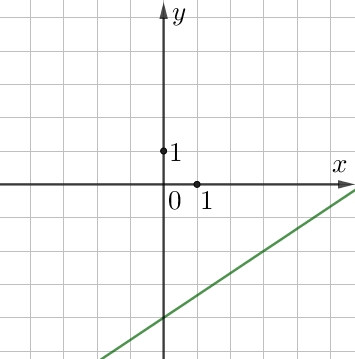
2. Теперь рассмотрим график \(\displaystyle Б\small.\)

Выберем на нём точку, которая не лежит на двух других графиках, и найдём уравнение, которому удовлетворяет эта точка. Оно и будет определять график \(\displaystyle Б\small.\)

Удобно взять на графике \(\displaystyle Б\) точку с целочисленными координатами, назовём её \(\displaystyle N(\green{0};\,\color{green}{-4}){\small .}\) Она не лежит на графике \(\displaystyle В\small.\)


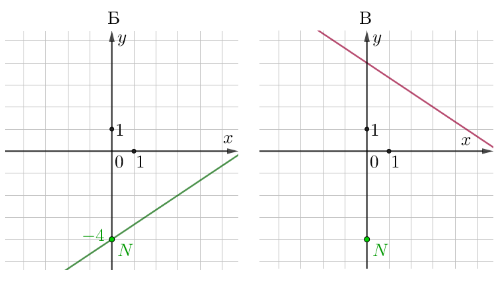
Подставим координаты точки \(\displaystyle N(\green{0};\,\color{green}{-4})\) в каждое из двух оставшихся уравнений.

Координаты точки \(\displaystyle N(0;\,-4)\) прямой \(\displaystyle Б\) удовлетворяют уравнению \(\displaystyle y=\frac{2}{3}x-4 {\small .}\)

Подставляя \(\displaystyle x=\green{0}\) и \(\displaystyle y=\color{green}{-4}\) в уравнение \(\displaystyle y=\frac{2}{3}x-4{\small ,}\) получаем:

\(\displaystyle \color{green}{-4}=\frac{2}{3}\cdot \green {0}-4{\small ;}\)
\(\displaystyle -4=-4\) (верно)

Координаты точки \(\displaystyle N(0;\,-4)\) прямой \(\displaystyle Б\) не удовлетворяют уравнению \(\displaystyle y=-\frac{2}{3}x+4 {\small .}\)

Следовательно, прямая \(\displaystyle Б\) имеет уравнение \(\displaystyle y=\frac{2}{3}x-4{\small .}\) 

Итак, установлены две пары прямая – уравнение:  

\(\displaystyle А\small:\) \(\displaystyle y=\frac{2}{3}x+4\) и \(\displaystyle Б\small:\) \(\displaystyle y=\frac{2}{3}x-4{\small .}\) 

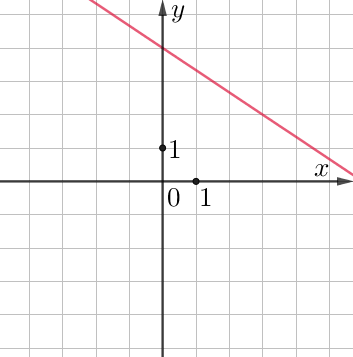
Тогда оставшаяся прямая \(\displaystyle В\) имеет уравнение \(\displaystyle y=-\frac{2}{3}x+4{\small .}\) 

Запишем ответ:

\(\displaystyle А\)\(\displaystyle Б\)\(\displaystyle В\)

\(\displaystyle y=\frac{2}{3}x+4\) 
 
\(\displaystyle y=\frac{2}{3}x-4\) 
 
\(\displaystyle y=-\frac{2}{3}x+4\)