Выберите функцию, графиком которой является данная прямая:
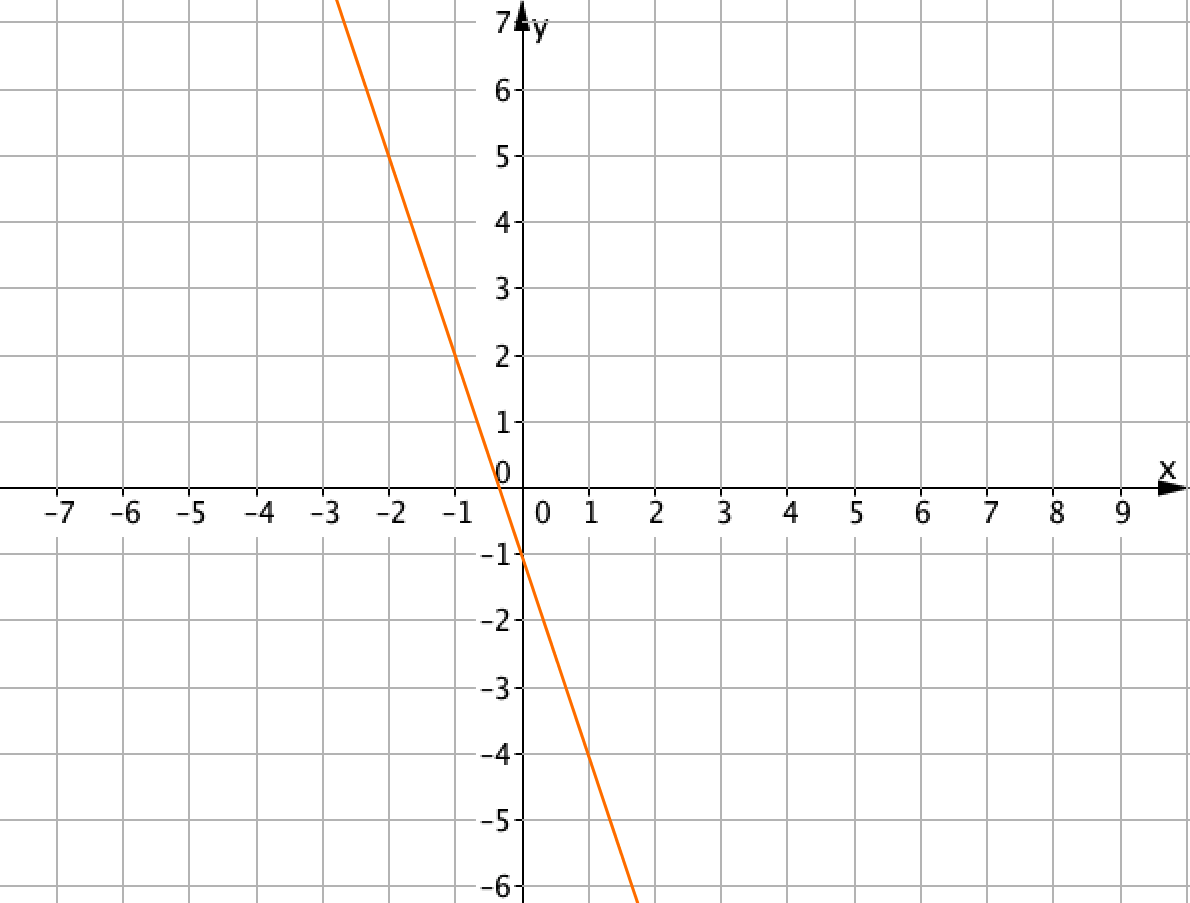
Так как графиком линейной функции является прямая, а прямая определяется двумя различными точками, то сперва выберем две различные точки на данной прямой.
Удобно выбрать точки \(\displaystyle \color{green}{A(0;\,-1)}\) и \(\displaystyle \color{red}{B(-1;\,2)}{\small :}\)
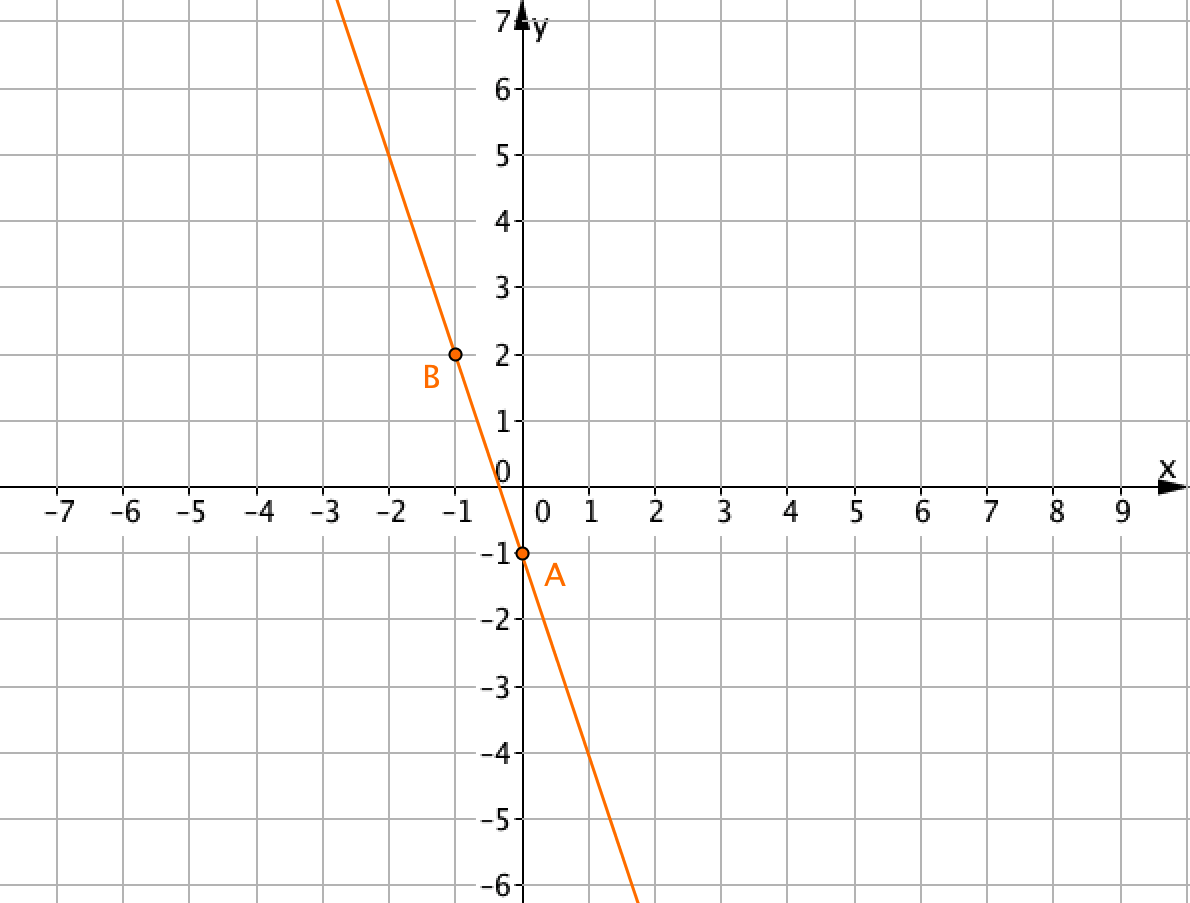
Если координаты точек \(\displaystyle \color{green}{A}\) и \(\displaystyle \color{red}{B}\) удовлетворяют уравнению, то это уравнение задает данную прямую.
Если координаты хотя бы одной из точек точек \(\displaystyle \color{green}{A}\) и \(\displaystyle \color{red}{B}\) не удовлетворяют уравнению, то это уравнение не задает данную прямую.
Подставим координаты точек в каждое из данных уравнений.
\(\displaystyle A(\color{blue}{0};\,\color{green}{-1}) {\small :}\) подставляя \(\displaystyle x=\color{blue}{0}\) и \(\displaystyle y=\color{green}{-1}\) в уравнение \(\displaystyle y=-3x-1{\small ,}\) получаем:
| \(\displaystyle \color{green}{-1}=-3\cdot \color{blue}{0}-1{\small ,}\) |
| \(\displaystyle \color{green}{-1}=-1\) – верное равенство. |
\(\displaystyle B(\color{blue}{-1};\,\color{green}{2}) {\small :}\) подставляя \(\displaystyle x=\color{blue}{-1}\) и \(\displaystyle y=\color{green}{2}\) в уравнение \(\displaystyle y=-3x-1{\small ,}\) получаем:
| \(\displaystyle \color{green}{2}=-3\cdot (\color{blue}{-1})-1{\small ,}\) |
| \(\displaystyle \color{green}{2}=2\) – верное равенство. |
Следовательно, уравнение \(\displaystyle y=-3x-1\) задает данную прямую.
Ответ: \(\displaystyle y=-3x-1{\small .}\)