Диагональ ромба равна \(\displaystyle 12\small,\) сторона ромба \(\displaystyle 10 \small.\) Найдите длину другой диагонали.
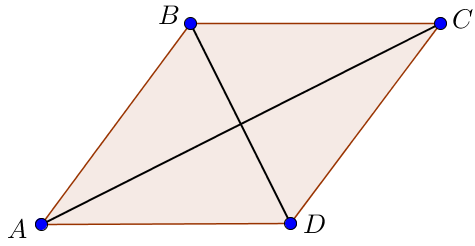
Пусть \(\displaystyle O\) – точка пересечения диагоналей ромба \(\displaystyle ABCD \small,\) дана диагональ \(\displaystyle BD=12\small.\)

По свойству параллелограмма диагонали точкой пересечения делятся пополам. Значит,
\(\displaystyle AO=OC\) и \(\displaystyle BO=OD=6 \small.\)
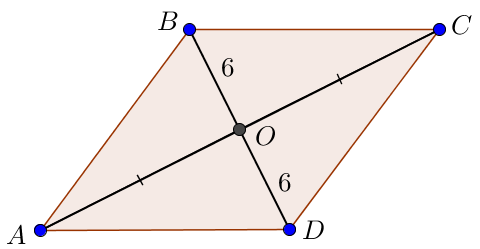
По свойству ромба диагонали перпендикулярны. Значит, угол \(\displaystyle AOB\) – прямой.
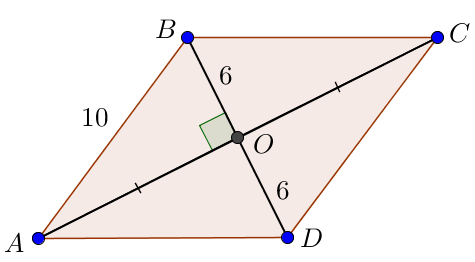
Рассмотрим прямоугольный треугольник \(\displaystyle AOB \small.\) Нам известны стороны \(\displaystyle AB=10\)
и \(\displaystyle BO=6 \small.\) Найдем сторону \(\displaystyle AO \small.\)
По теореме Пифагора
\(\displaystyle AO^2=AB^2-OB^2 \small.\)
Тогда
\(\displaystyle AO^2=10^2-6^2=100-36=64\small.\)
Поскольку длина отрезка положительна, то \(\displaystyle AO=8 \small.\)
Значит, \(\displaystyle AC=2\cdot AO=16 {\small .}\)
Ответ: \(\displaystyle 16 {\small .}\)