В ромбе \(\displaystyle ABCD\) сторона равна \(\displaystyle 4 \small,\) угол \(\displaystyle BAD\) равен \(\displaystyle 60^\circ \small.\) Найдите диагональ \(\displaystyle BD\) ромба.

Рассмотрим \(\displaystyle \triangle BAD \small. \) Поскольку стороны ромба равны, то \(\displaystyle AB = AD \small.\) Тогда треугольник \(\displaystyle BAD \) – равнобедренный, а угол при вершине равен \(\displaystyle \angle BAD = 60^{\circ} \small.\)
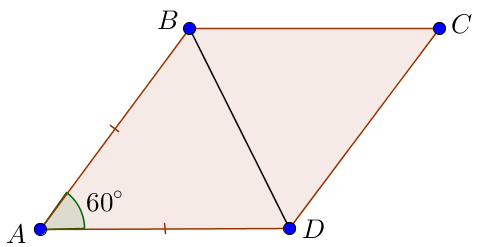
По свойству равнобедренного треугольника углы при основании равны:
\(\displaystyle \angle ADB = \angle ABD \small.\)
Поскольку сумма углов треугольника составляет \(\displaystyle 180^{\circ} \small,\) то
\(\displaystyle \angle ADB = \angle ABD =\frac{180^{\circ} - \angle BAD}{2}= \frac{180^{\circ} - 60^{\circ}}{2}= \frac{120^{\circ}}{2}= 60^{\circ} \small.\)
Получили, что все углы в треугольнике \(\displaystyle BAD \) равны \(\displaystyle 60^{\circ} \small. \)
Значит, треугольник \(\displaystyle BAD \) – равносторонний, \(\displaystyle BD = 4 \small.\)
Ответ: \(\displaystyle 4 {\small .}\)