Skip to main content

Теория: 03 Площадь треугольника

Задание

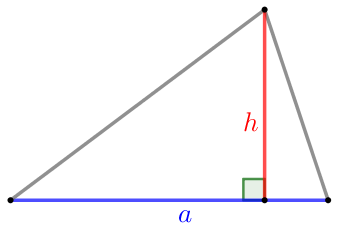
У треугольника со сторонами \(\displaystyle 6\) и \(\displaystyle 8\) провели высоты к этим сторонам. Высота, проведённая  к первой стороне, равна \(\displaystyle 4 {\small.}\)  Чему равна высота, проведённая ко второй стороне?

Решение

 

Пусть в треугольнике \(\displaystyle ABC{\small:}\)

  • \(\displaystyle AC=6 {\small,}\) \(\displaystyle BH=4 \) – высота, проведённая к стороне \(\displaystyle AC {\small;}\) 
  • \(\displaystyle BC=8 {\small,}\) \(\displaystyle AK=\color{red} {h} \) – высота, проведённая к стороне \(\displaystyle BC {\small.}\)

 

Воспользуемся формулой площади треугольника.

Найдем площадь треугольника \(\displaystyle ABC\) двумя способами:

\(\displaystyle 1\) СПОСОБ
\(\displaystyle 2\) СПОСОБ

 

\(\displaystyle S_{\triangle ABC}= \frac{1}{2} \cdot BH \cdot AC {\small,} \)

\(\displaystyle S_{\triangle ABC}= \frac{1}{2} \cdot 4 \cdot 6 =12{\small.} \)

 

\(\displaystyle S_{\triangle ABC}= \frac{1}{2} \cdot AK \cdot BC {\small,} \)

\(\displaystyle S_{\triangle ABC}= \frac{1}{2} \cdot \color{red} {h} \cdot 8 =4 \cdot \color{red} {h}{\small.} \)

 

Получаем

\(\displaystyle 12=4 \cdot \color{red} {h} {\small,}\)

\(\displaystyle \color{red} {h}=3 {\small.}\)

Ответ: \(\displaystyle 3 {\small.}\)