Основания прямоугольной трапеции равны \(\displaystyle 18\) и \(\displaystyle 24\small,\) площадь равна \(\displaystyle 168\small.\) Найдите её меньшую боковую сторону.
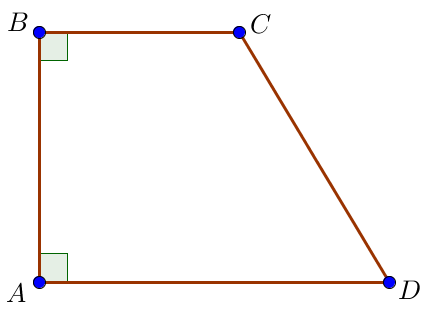
Пусть \(\displaystyle ABCD\) – прямоугольная трапеция с прямыми углами \(\displaystyle A\) и \(\displaystyle B\) и тупым углом \(\displaystyle C\small.\)
Тогда ее основания \(\displaystyle BC=18\) и \(\displaystyle AD=24\small,\) меньшая боковая сторона \(\displaystyle AB\small.\)
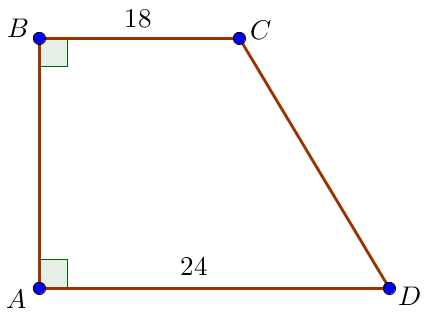
Так как \(\displaystyle AB\) перпендикулярна основаниям трапеции, то \(\displaystyle AB\) является высотой трапеции.
Требуется найти \(\displaystyle AB\small.\)
Поскольку площадь трапеции равна произведению полусуммы оснований на высоту,
\(\displaystyle S=\frac{AD+BC}{2} \cdot AB \small,\)
то
\(\displaystyle {168} = \frac{{24}+{18}}{2}\cdot AB {\small.}\)
Тогда
\(\displaystyle {168} = 21\cdot AB \, \ \bigg| : \color{red}{21}{\small,}\)
\(\displaystyle AB={8}{\small . }\)
Ответ: \(\displaystyle 8{\small .}\)