Диагонали трапеции перпендикулярны и равны \(\displaystyle 8\) и \(\displaystyle 7 \small.\) Найдите площадь трапеции.
Воспользуемся одной из формул для вычисления площади трапеции.
Формула площади трапеции
\(\displaystyle S=\frac{d_1 \cdot d_2}{2} \cdot \sin \varphi \small,\)
где \(\displaystyle d_1\) и \(\displaystyle d_2\) – диагонали трапеции,
\(\displaystyle \varphi \) – угол между диагоналями трапеции.
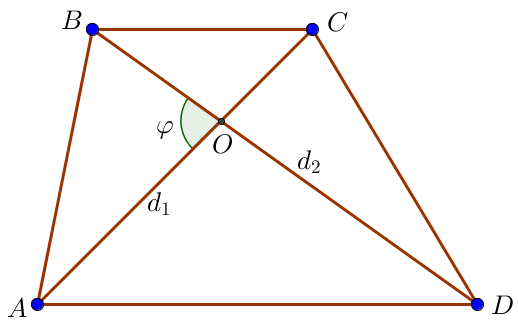
В данном случае \(\displaystyle d_1=8 \small,\) \(\displaystyle d_2=7 \small,\) \(\displaystyle \varphi = 90^{\circ} {\small : } \)
\(\displaystyle {S_{трап}} = \frac{8 \cdot 7}{2} \cdot \sin 90^{\circ} =\frac{56}{2} \cdot 1=28 {\small.}\)
Ответ: \(\displaystyle 28{\small .}\)