Найдите площадь прямоугольной трапеции, основания которой равны \(\displaystyle 6\) и \(\displaystyle 4 \small,\) большая боковая сторона составляет с основанием угол \(\displaystyle 45^\circ \small.\)
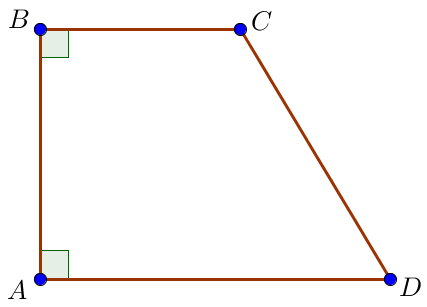
Пусть \(\displaystyle ABCD\) – прямоугольная трапеция с прямыми углами \(\displaystyle A\) и \(\displaystyle B\\ \)и основаниями \(\displaystyle BC=4\) и \(\displaystyle AD=6 \small,\) \(\displaystyle \angle D=45^{\circ} \small.\)
Опустим высоту \(\displaystyle CH \small.\) В четырехугольнике \(\displaystyle ABCH\) все углы прямые, поэтому он является прямоугольником. Значит, \(\displaystyle AH=BC=4 \small.\) Тогда \(\displaystyle HD=AD-AH=6-4=2 \small.\) | 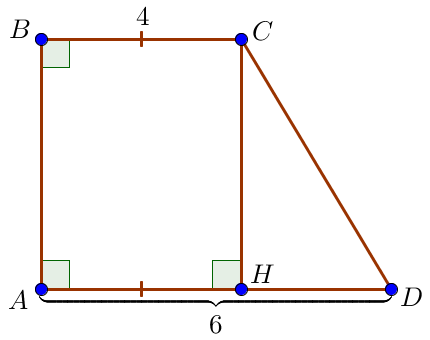 |
Рассмотрим треугольник \(\displaystyle CHD \small.\) Нам известны углы \(\displaystyle \angle CHD=90^{\circ}\) и \(\displaystyle \angle HDC=45^{\circ} \small.\) Поскольку сумма углов треугольника равна \(\displaystyle 180^{\circ} \small,\) то \(\displaystyle \angle HCD=180^{\circ}-\angle CHD - \angle HDC \small, \) \(\displaystyle \angle HCD=180^{\circ}-90^{\circ}-45^{\circ}=45^{\circ} \small. \)
\(\displaystyle CH=HD=2\small.\) | 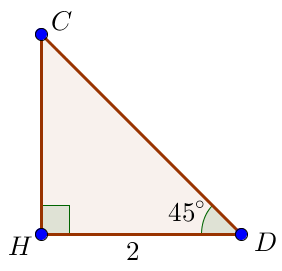 |
Так как площадь трапеции равна произведению полусуммы оснований на высоту, то
\(\displaystyle {S_{ABCD}} = \frac{{AD}+{BC}}{2}\cdot {CH} =\frac{{6}+{4}}{2}\cdot {2} = \frac{10}{2}\cdot {2} =10 {\small .}\)
Ответ: \(\displaystyle 10 \small.\)