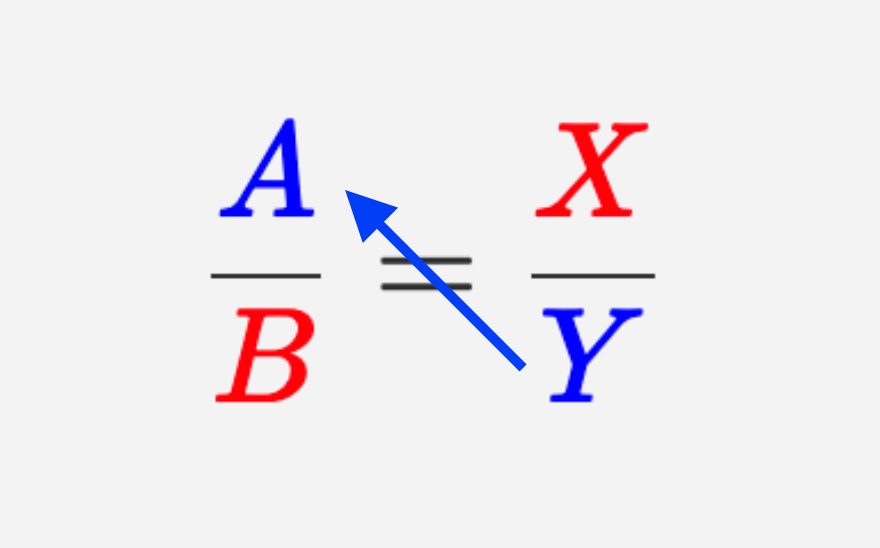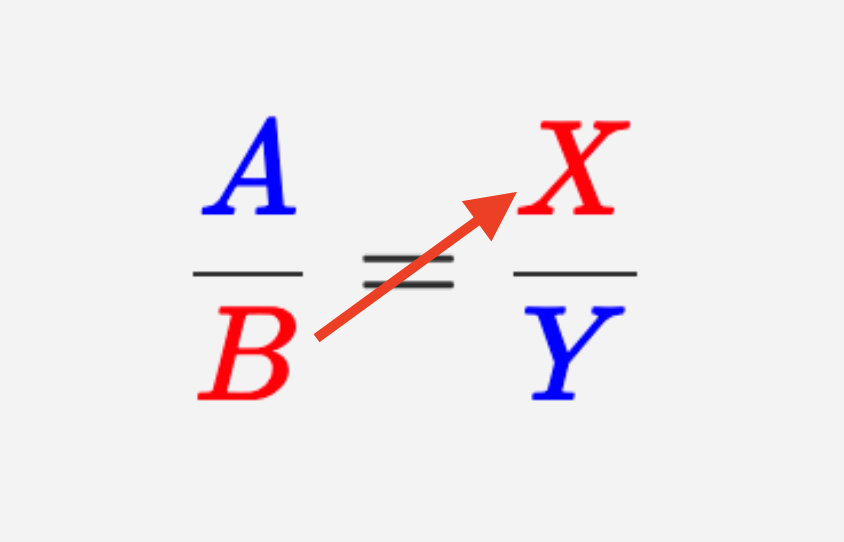Решите уравнение
\(\displaystyle \sqrt{\frac{1}{14-5x}}=\frac{1}{3}{\small .}\)
Способ 1
Для решения уравнения \(\displaystyle \sqrt{\frac{1}{14-5x}}=\frac{1}{3}\) возведем обе части в квадрат.
При этом могут появиться посторонние корни, поэтому после решения необходима проверка.
Получаем:
\(\displaystyle \left(\sqrt{\frac{1}{14-5x}}\right)^2=\left(\frac{1}{3}\right)^2{\small ,}\)
\(\displaystyle \frac{1}{14-5x}=\frac{1}{9}{\small .}\)
Перемножим дроби по правилу пропорции.
\(\displaystyle \frac{\color{blue}{1}}{\color{red}{{14-5x}}}=\frac{\color{red}{1}}{\color{blue}{9}}{\small ,}\)
\(\displaystyle \color{blue}{1}\cdot \color{blue}{9}=\color{red}{1}\cdot (\color{red}{{14-5x}}){\small ,}\)
\(\displaystyle 14-5x=9{\small .}\)
Решим полученное линейное уравнение:
\(\displaystyle -5x=9-14{\small ,}\)
\(\displaystyle -5x=-5{\small ,}\)
\(\displaystyle x=1{\small .}\)
Проверка: подставим \(\displaystyle x=1\) в исходное уравнение. Получаем:
\(\displaystyle \sqrt{\frac{1}{14-5\cdot 1}}=\frac{1}{3}{\small ;}\)
\(\displaystyle \sqrt{\frac{1}{9}}=\frac{1}{3}{\small ;}\)
\(\displaystyle \frac{1}{3}=\frac{1}{3}\) – верно.
Ответ:\(\displaystyle 1{\small .}\)
Способ 2
Заметим, что по свойству корней \(\displaystyle \sqrt{\frac{1}{14-5x}}=\frac{\sqrt{1}}{\sqrt{14-5x}}=\frac{1}{\sqrt{14-5x}}{\small .}\)
Следовательно, получили уравнение
\(\displaystyle \frac{1}{\sqrt{14-5x}}=\frac{1}{3}{\small .}\)
Перемножим дроби по правилу пропорции, а затем сделаем проверку.
Получаем:
\(\displaystyle \frac{\color{blue}{1}}{\color{red}{\sqrt{14-5x}}}=\frac{\color{red}{1}}{\color{blue}{3}}{\small ,}\)
\(\displaystyle \color{blue}{1}\cdot \color{blue}{3}=\color{red}{1}\cdot \color{red}{\sqrt{14-5x}}{\small ,}\)
\(\displaystyle 3=\sqrt{14-5x}{\small ,}\)
\(\displaystyle \sqrt{14-5x}=3{\small .}\)
Для решения уравнения \(\displaystyle \sqrt{14-5x}=3\) возведем обе части в квадрат.
Получаем:
\(\displaystyle (\sqrt{14-5x})^2=3^2{\small ,}\)
\(\displaystyle 14-5x=9{\small .}\)
Решим полученное линейное уравнение:
\(\displaystyle -5x=9-14{\small ,}\)
\(\displaystyle -5x=-5{\small ,}\)
\(\displaystyle x=1{\small .}\)
Проверка: подставим \(\displaystyle x=1\) в исходное уравнение. Получаем:
\(\displaystyle \sqrt{\frac{1}{14-5\cdot 1}}=\frac{1}{3}{\small ;}\)
\(\displaystyle \sqrt{\frac{1}{9}}=\frac{1}{3}{\small ;}\)
\(\displaystyle \frac{1}{3}=\frac{1}{3}\) – верно.
Ответ:\(\displaystyle 1{\small .}\)