В треугольнике \(\displaystyle ABC\) угол \(\displaystyle \angle A\) равен \(\displaystyle 60^\circ{\small , }\) угол \(\displaystyle \angle B\) равен \(\displaystyle 82^\circ{\small , }\) \(\displaystyle AD,\, BE\) и \(\displaystyle CF\) – биссектрисы, пересекающиеся в точке \(\displaystyle O{\small .}\) Найдите угол \(\displaystyle AOF{\small .}\)
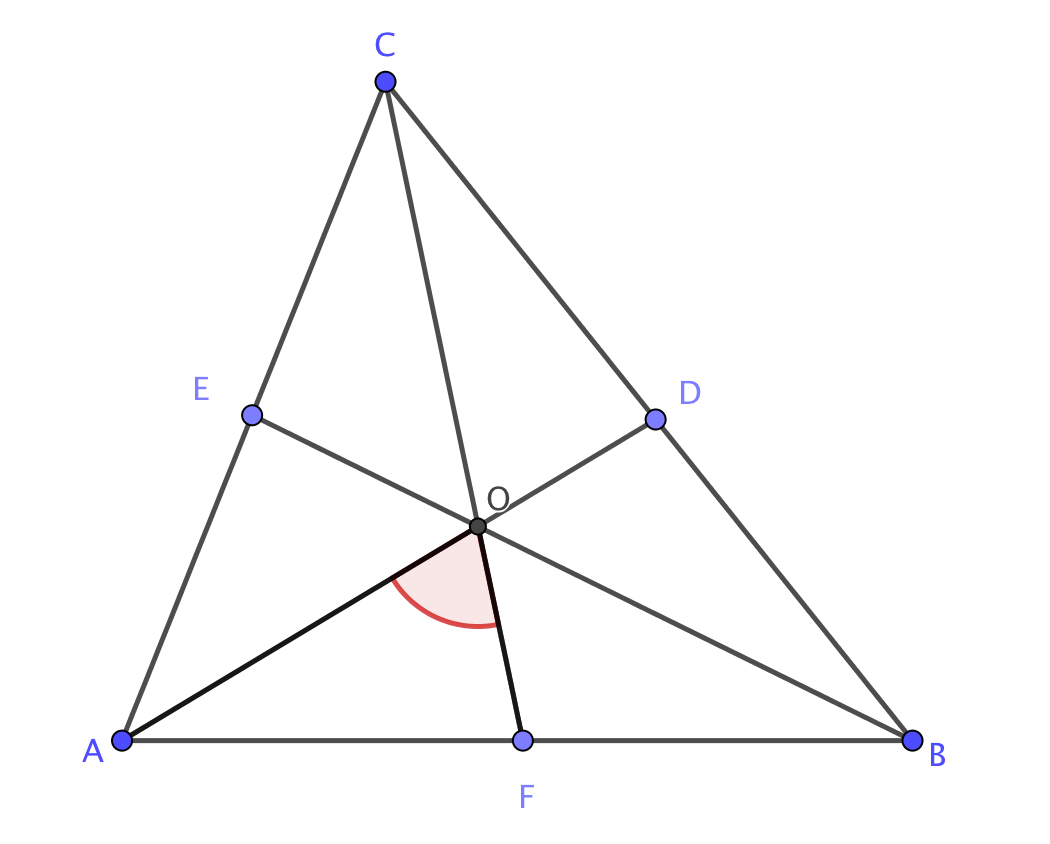
\(\displaystyle \angle AOF=\)\(\displaystyle ^\circ\)
По условию нужно найти угол \(\displaystyle AOF{\small . } \)
Заметим, что искомый угол \(\displaystyle AOF\) является внешним углом треугольника \(\displaystyle AOC\) при вершине \(\displaystyle O{\small . }\)
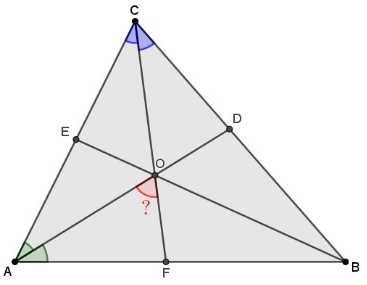
Поскольку сумма углов в треугольнике равна \(\displaystyle 180^\circ{\small ,} \) то в треугольнике \(\displaystyle ABC \) угол \(\displaystyle C \) равен
\(\displaystyle \angle C=180-\angle A- \angle B= 180^\circ- 60^\circ- 82^\circ= 38^\circ{\small . } \)
Так как \(\displaystyle AD\) и \(\displaystyle CF\) – биссектрисы, то получаем следующие значения углов в треугольнике \(\displaystyle AOC{\small :}\)
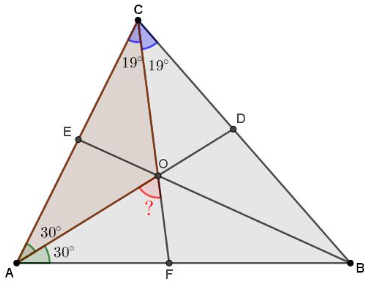
Так как внешний угол треугольника равен сумме двух не смежных с ним внутренних углов, то
\(\displaystyle \angle AOF=\angle BAO+\angle AСO=30^\circ+19^\circ=49^\circ{\small . }\)
Ответ: \(\displaystyle 49^\circ{\small .} \)