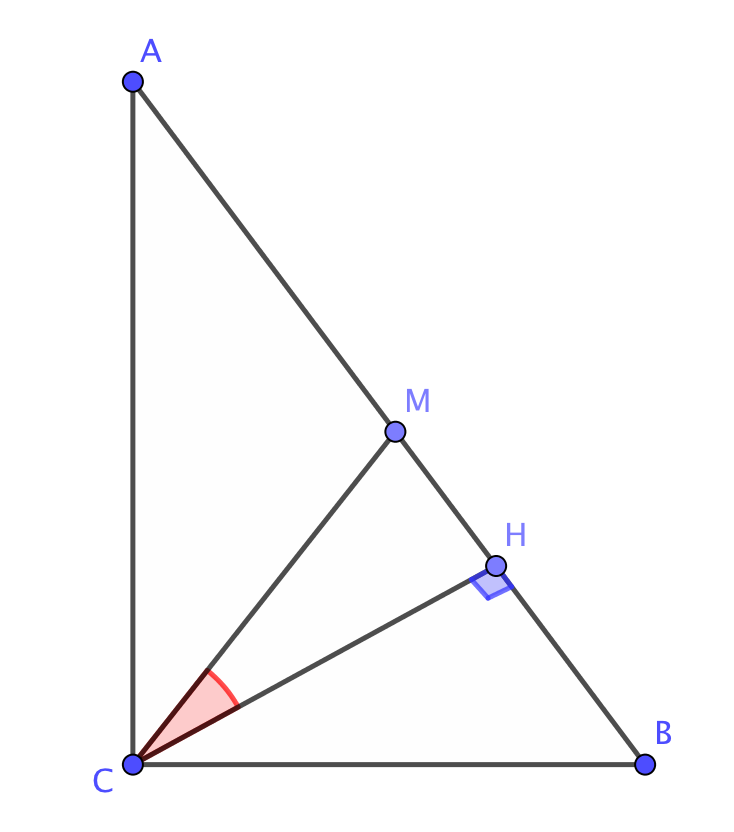
В прямоугольном треугольнике \(\displaystyle ABC\) угол между высотой \(\displaystyle CH\) и медианой \(\displaystyle CM{\small , }\) проведенными из вершины прямого угла, равен \(\displaystyle 40^\circ{\small .}\) Найдите больший из острых углов прямоугольного треугольника \(\displaystyle ABC{\small .}\)
\(\displaystyle ^\circ\)
В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы.
Поэтому \(\displaystyle CM= AM= MB{\small .} \)
Обозначим угол \(\displaystyle B \) через \(\displaystyle \alpha{\small .} \) Так как \(\displaystyle \triangle CHB \) – прямоугольный, то \(\displaystyle \angle HCB= 90^\circ- \alpha{\small .} \)
\(\displaystyle \angle C= 90^\circ \) и \(\displaystyle \angle C= \angle ACM+ \angle MCH+ \angle HCB{\small , } \)
\(\displaystyle 90^\circ= \angle ACM+ 40^\circ+ 90^\circ- \alpha{\small , } \)
\(\displaystyle \angle ACM= \alpha- 40^\circ{\small .} \)
\(\displaystyle \triangle ACM \) – равнобедренный. Значит, \(\displaystyle \angle A= \angle MCA= \alpha- 40^\circ{\small .} \)
Получаем, что \(\displaystyle \angle B= \alpha \) и \(\displaystyle \angle A= \alpha- 40^\circ{\small .} \)
Так как \(\displaystyle \angle B+ \angle A= 90^\circ{\small , } \) то получаем:
\(\displaystyle \alpha+ \alpha- 40^\circ= 90^\circ{\small ,} \)
\(\displaystyle 2\alpha= 90^\circ+ 40^\circ {\small , }\)
\(\displaystyle 2\alpha= 130^\circ {\small , }\)
\(\displaystyle \alpha= 65^\circ {\small . }\)
Таким образом,
\(\displaystyle \angle B= 65^\circ{\small , } \)
\(\displaystyle \angle A= 90^\circ-65^\circ= 25^\circ{\small .} \)
Больший угол равен \(\displaystyle 65^\circ{\small .} \)
Ответ: \(\displaystyle 65^\circ{\small .} \)