Задание
В треугольнике \(\displaystyle ABC\) угол \(\displaystyle C\) прямой, \(\displaystyle AC=3,\) \(\displaystyle BC=4.\) Найдите длину вектора \(\displaystyle \overrightarrow {AC}+\overrightarrow {CB}.\)
Решение
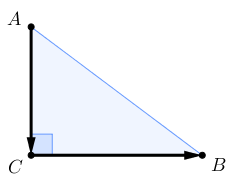
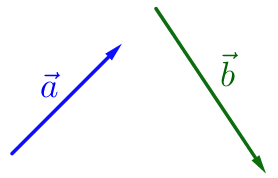Изобразим данный треугольник и указанные в условии векторы.
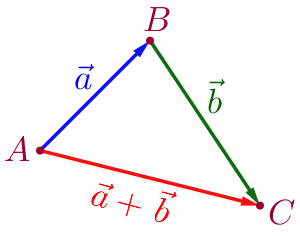
По правилу треугольника
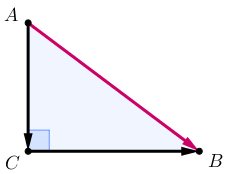
\(\displaystyle \overrightarrow {AC}+\overrightarrow {CB}=\color{#CC0066}{\overrightarrow {AB}}.\)
Длина вектора \(\displaystyle \color{#CC0066}{\overrightarrow {AB}}\) равна длине отрезка \(\displaystyle AB.\)
По теореме Пифагора из прямоугольного треугольника \(\displaystyle ABC\)
\(\displaystyle AB^2=AC^2+BC^2.\)
Значит,
\(\displaystyle AB^2=3^2+4^2=9+16=25=5^2,\)
\(\displaystyle AB=5.\)
Следовательно, \(\displaystyle |\overrightarrow {AB}|=AB=5.\)
Ответ: \(\displaystyle 5.\)