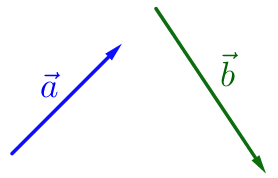Перейдем от операции вычитания векторов к операции сложения. Так как
\(\displaystyle \color{#009900}{\overrightarrow {AC}}=-\overrightarrow {CA},\)
то
\(\displaystyle \overrightarrow {CB}-\overrightarrow {CA}=\overrightarrow {CB}+\color{#009900}{\overrightarrow {AC}}.\)
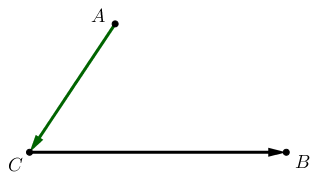
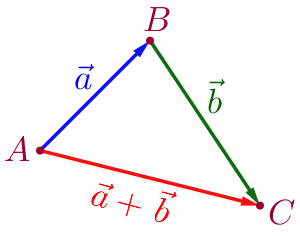
По свойству суммы векторов
\(\displaystyle \overrightarrow {CB}+\color{#009900}{\overrightarrow {AC}}=\color{#009900}{\overrightarrow {AC}}+\overrightarrow {CB}.\)
По правилу треугольника
правило треугольникаДля сложения двух векторов \(\displaystyle \vec{a}\) и \(\displaystyle \vec{b}\) необходимо:
- отложить от какой-нибудь точки \(\displaystyle A\) вектор \(\displaystyle \overrightarrow {AB}{\small,}\) равный \(\displaystyle \vec{a}{\small;}\)
- от точки \(\displaystyle B\) отложить вектор \(\displaystyle \overrightarrow {BC}{\small,}\) равный \(\displaystyle \vec{b}{\small;}\)
- вектор \(\displaystyle \overrightarrow {AC}\) называется суммой векторов \(\displaystyle \vec{a}\) и \(\displaystyle \vec{b}{\small.}\)
Правило треугольника можно сформулировать также следующим образом:
Правило треугольникаЕсли \(\displaystyle A{\small,}\) \(\displaystyle B\) и \(\displaystyle C\) – произвольные точки, то
\(\displaystyle \overrightarrow {AB}+\overrightarrow {BC}=\overrightarrow {AC}{\small.}\)
Это равенство справедливо для произвольных точек \(\displaystyle A{\small,}\) \(\displaystyle B\) и \(\displaystyle C\) (даже если две или все три точки совпадают).

\(\displaystyle \color{#009900}{\overrightarrow {AC}}+\overrightarrow {CB}=\color{#CC0066}{\overrightarrow {AB}}.\)
Ответ: \(\displaystyle \overrightarrow {AB}.\)