Способ 1 (решение неравенств методом интервалов)
Каждый из ответов является решением одного из неравенств в условии.
По очереди найдем ответы первых трех неравенств.
Последний оставшийся ответ будет решением четвертого неравенства.
Рассмотрим неравенства в порядке увеличения сложности решения методом интервалов.
Решение неравенства \(\displaystyle (x-1)(x-2)<0{\small :}\) \(\displaystyle 1 < x < 2{\small .}\)
1. Найдем корни выражения \(\displaystyle (x-1)(x-2){\small :}\)
\(\displaystyle x-1=0\) или \(\displaystyle x-2=0{\small ,}\)
\(\displaystyle x=1\) или \(\displaystyle x=2{\small .}\)
2. Расставим на числовой оси точки, соответствующие найденным корням.
Неравенство строгое, поэтому нули числителя и знаменателя изображаются выколотыми точками:
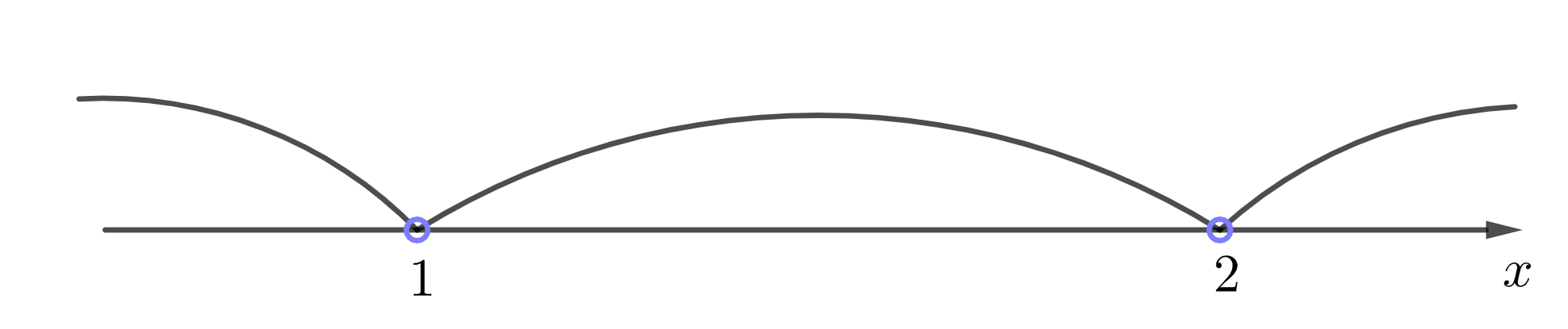
3. Получили три интервала, на которых нужно определить знаки:
\(\displaystyle (-\infty;1){\small ,}\) \(\displaystyle (1;2)\) и \(\displaystyle (2;+\infty){\small .}\)
Тогда для \(\displaystyle f(x)=(x-1)(x-2)\) получаем:
\(\displaystyle f(-2)>0\quad\quad\quad\quad\quad f(1{,}5)<0\quad\quad\quad\quad\quad f(3)>0\)
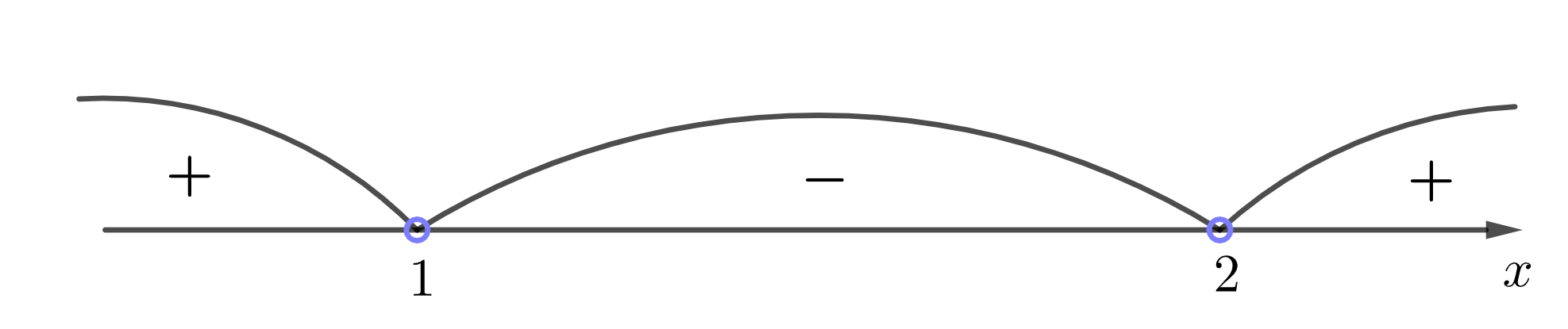
Решения неравенства \(\displaystyle (x-1)(x-2)<0\) соответствуют промежуткам, где функция отрицательна, откуда
\(\displaystyle 1 < x < 2\)– искомое решение.
Решение неравенства \(\displaystyle \frac{x-1}{x-2}>0{\small :}\) \(\displaystyle x<1\) или \(\displaystyle x>2{\small .}\)
1. Найдем корни числителя и знаменателя дроби \(\displaystyle \frac{x-1}{x-2}{\small :}\)
\(\displaystyle x-1=0\) или \(\displaystyle x-2=0{\small ,}\)
\(\displaystyle x=1\) или \(\displaystyle x=2{\small .}\)
2. Расставим на числовой оси точки, соответствующие найденным корням.
Неравенство строгое, поэтому нули числителя и знаменателя изображаются выколотыми точками:

3. Получили три интервала, на которых нужно определить знаки:
\(\displaystyle (-\infty;1){\small ,}\) \(\displaystyle (1;2)\) и \(\displaystyle (2;+\infty){\small .}\)
Тогда для \(\displaystyle f(x)=\frac{x-1}{x-2}\) получаем:
\(\displaystyle f(-2)>0\quad\quad\quad\quad\quad f(1{,}5)<0\quad\quad\quad\quad\quad f(3)>0\)

Решения неравенства \(\displaystyle \frac{x-1}{x-2}>0\) соответствуют промежуткам, где функция положительна, откуда
\(\displaystyle x<1\) или \(\displaystyle x>2\)– искомое решение.
Решение неравенства \(\displaystyle (x-1)^2(x-2)<0{\small :}\) \(\displaystyle x<1\) или \(\displaystyle 1 < x < 2{\small .}\)
1. Найдем корни выражения \(\displaystyle (x-1)^2(x-2){\small :}\)
\(\displaystyle (x-1)^2=0\) или \(\displaystyle x-2=0{\small ,}\)
\(\displaystyle x=1\) или \(\displaystyle x=2{\small .}\)
2. Расставим на числовой оси точки, соответствующие найденным корням.
Неравенство строгое, поэтому нули числителя и знаменателя изображаются выколотыми точками:

3. Получили три интервала, на которых нужно определить знаки:
\(\displaystyle (-\infty;1){\small ,}\) \(\displaystyle (1;2)\) и \(\displaystyle (2;+\infty){\small .}\)
Тогда для \(\displaystyle f(x)=(x-1)^2(x-2)\) получаем:
\(\displaystyle f(-2)<0\quad\quad\quad\quad\quad f(1{,}5)<0\quad\quad\quad\quad\quad f(3)>0\)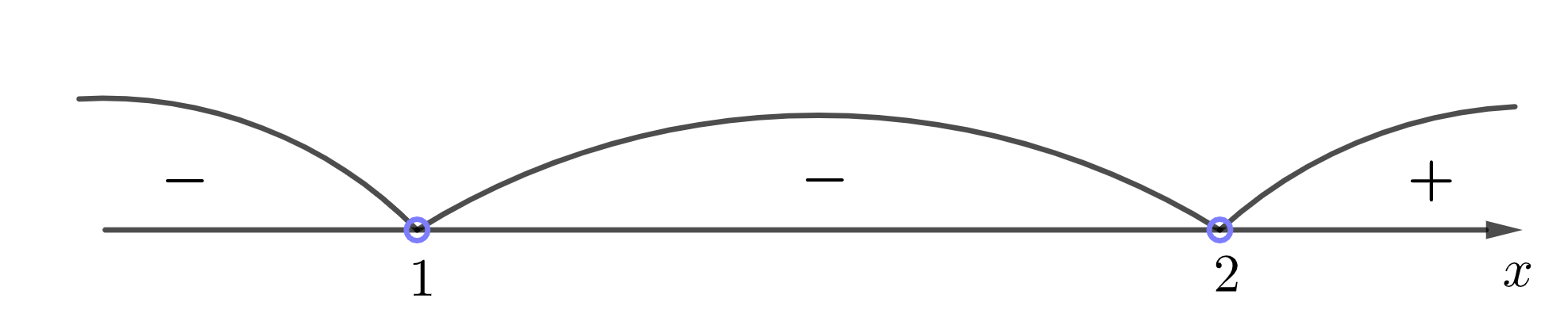
Решения неравенства \(\displaystyle (x-1)^2(x-2)<0\) соответствуют промежуткам, где функция отрицательна, откуда
\(\displaystyle x<1\) или \(\displaystyle 1 < x < 2\)– искомое решение.
Следовательно, решением неравенства \(\displaystyle \frac{(x-2)^2}{x-1}>0\) является единственный оставшийся ответ \(\displaystyle 1 < x < 2\) или \(\displaystyle x>2{\small .}\)
Ответ: решением неравенства \(\displaystyle (x-1)(x-2)<0\) является \(\displaystyle 1 < x < 2{\small ,}\)
решением неравенства \(\displaystyle \frac{x-1}{x-2}>0\) является \(\displaystyle x<1\) или \(\displaystyle x>2{\small ,}\)
решением неравенства \(\displaystyle (x-1)^2(x-2)<0\) является \(\displaystyle x<1\) или \(\displaystyle 1 < x < 2{\small ,}\)
решением неравенства \(\displaystyle \frac{(x-2)^2}{x-1}>0\) является \(\displaystyle 1 < x < 2\) или \(\displaystyle x>2{\small .}\)
Способ 2 (решение с помощью систем неравенств)
Каждый из ответов является решением одного из неравенств в условии.
По очереди найдем ответы первых трех неравенств.
Последний оставшийся ответ будет решением четвертого неравенства.
Рассмотрим неравенства в порядке увеличения сложности решения.
Решение неравенства \(\displaystyle (x-1)(x-2)<0{\small :}\) \(\displaystyle 1 < x < 2{\small .}\)
Левая часть неравенства состоит из произведения двух множителей: \(\displaystyle x-1\) и \(\displaystyle x-2{\small .}\)
Так как произведение отрицательно, множители должны иметь разные знаки.
Следовательно, возможны ситуации:
\(\displaystyle \begin{cases}x-1>0{\small ,}\\x-2<0{\small ;}\end{cases}\) | или | \(\displaystyle \begin{cases}x-1<0{\small ,}\\x-2>0{\small .}\end{cases}\) |
Решим полученные системы:
\(\displaystyle \begin{cases}x>1{\small ,}\\x<2{\small ;}\end{cases}\) | или | \(\displaystyle \begin{cases}x<1{\small ,}\\x>2{\small .}\end{cases}\) |
Нарисуем эти условия на одной числовой оси:
\(\displaystyle \color{green}{x<2}\quad\quad\quad\quad\quad\quad\quad\quad\quad \color{red}{x>1}\) 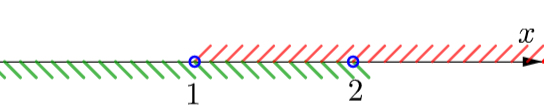
| или | \(\displaystyle \color{red}{x<1}\quad\quad\quad\quad\quad\quad\quad\quad\quad \color{green}{x>2}\) 
|
Решением является пересечение, то есть та область, где есть штриховка и сверху, и снизу:
| \(\displaystyle x\in(1;2)\) | или | решений нет. |
Следовательно, \(\displaystyle x\in(1;2){\small .}\)
Решение неравенства \(\displaystyle \frac{x-1}{x-2}>0{\small :}\) \(\displaystyle x<1\) или \(\displaystyle x>2{\small .}\)
Левая часть неравенства является дробью с числителем \(\displaystyle x-1\) и знаменателем \(\displaystyle x-2{\small .}\)
Так как дробь положительна, числитель и знаменатель должны иметь одинаковые знаки.
Следовательно, возможны ситуации:
\(\displaystyle \begin{cases}x-1>0{\small ,}\\x-2>0{\small ;}\end{cases}\) | или | \(\displaystyle \begin{cases}x-1<0{\small ,}\\x-2<0{\small .}\end{cases}\) |
Решим полученные системы:
\(\displaystyle \begin{cases}x>1{\small ,}\\x>2{\small ;}\end{cases}\) | или | \(\displaystyle \begin{cases}x<1{\small ,}\\x<2{\small .}\end{cases}\) |
Нарисуем эти условия на одной числовой оси:
\(\displaystyle \quad\quad\quad\quad\quad\quad\quad\quad\quad \color{red}{x>1}\) \(\displaystyle \quad\quad\quad\quad\quad\quad\quad\quad\quad \color{green}{x>2}\) | или | \(\displaystyle \color{red}{x<1}\quad\quad\quad\quad\quad\quad\quad\quad\quad \) 
\(\displaystyle \color{green}{x<2}\quad\quad\quad\quad\quad\quad\quad\quad\quad \) |
Решением является пересечение, то есть та область, где есть штриховка и сверху, и снизу:
| \(\displaystyle x\in(2;+\infty)\) | или | \(\displaystyle x\in(-\infty;1){\small . }\) |
Следовательно, \(\displaystyle x\in(-\infty;1)\cup(2;+\infty){\small .}\)
Решение неравенства \(\displaystyle (x-1)^2(x-2)<0{\small :}\) \(\displaystyle x<1\) или \(\displaystyle 1 < x < 2{\small .}\)
Левая часть неравенства состоит из произведения двух множителей: \(\displaystyle (x-1)^2\) и \(\displaystyle x-2{\small .}\)
Так как произведение отрицательно, множители должны иметь разные знаки.
Следовательно, возможны ситуации:
\(\displaystyle \begin{cases}(x-1)^2>0{\small ,}\\x-2<0{\small ;}\end{cases}\) | или | \(\displaystyle \begin{cases}(x-1)^2<0{\small ,}\\x-2>0{\small .}\end{cases}\) |
Рассмотрим решение первого неравенства в обеих системах.
\(\displaystyle (x-1)^2\) – это квадрат числа, который всегда неотрицателен.
Значит, первое неравенство \(\displaystyle (x-1)^2>0\) верно при \(\displaystyle x-1\,\cancel{=}\,0{\small .}\)
Соответственно, второе неравенство \(\displaystyle (x-1)^2<0\) не будет выполняться не при каких \(\displaystyle x{\small .}\)
Учитывая полученное, перепишем эти две системы:
\(\displaystyle \begin{cases}x\,\cancel{=}\,1{\small ,}\\x<2{\small ;}\end{cases}\) | или | решений нет. |
У второй системы нет решений. Значит, продолжим решать только первую систему.
Нарисуем эти условия на одной числовой оси:
\(\displaystyle \color{green}{x<2}\quad\quad\quad\quad\quad\quad\quad \color{red}{x\,\cancel{=}\,1}\)
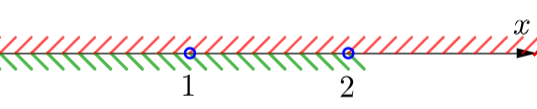
Решением является пересечение, то есть та область, где есть штриховка и сверху, и снизу:
Следовательно, \(\displaystyle x\in (-\infty;1)\cup(1;2){\small .}\)
Следовательно, решением неравенства \(\displaystyle \frac{(x-2)^2}{x-1}>0\) является единственный оставшийся ответ \(\displaystyle 1 < x < 2\) или \(\displaystyle x>2{\small .}\)
Ответ: решением неравенства \(\displaystyle (x-1)(x-2)<0\) является \(\displaystyle 1 < x < 2{\small ,}\)
решением неравенства \(\displaystyle \frac{x-1}{x-2}>0\) является \(\displaystyle x<1\) или \(\displaystyle x>2{\small ,}\)
решением неравенства \(\displaystyle (x-1)^2(x-2)<0\) является \(\displaystyle x<1\) или \(\displaystyle 1 < x < 2{\small ,}\)
решением неравенства \(\displaystyle \frac{(x-2)^2}{x-1}>0\) является \(\displaystyle 1 < x < 2\) или \(\displaystyle x>2{\small .}\)


