Требуется решить неравенство:
\(\displaystyle \frac{-10}{(x-3)^2-5}\geqslant 0{\small.}\)
Рассмотрим выражение в левой части неравенства.
- числитель дроби \(\displaystyle -10\) – отрицателен \(\displaystyle (-10<0){\small ;}\)
- знаменатель \(\displaystyle (x-3)^2-5\,\cancel=\, 0{\small.}\)
Чтобы значение дроби было неотрицательным, требуется, чтобы ее знаменатель был отрицательным:
\(\displaystyle (x-3)^2-5< 0{\small.}\)
Используя формулу разности квадратов, разложим левую часть неравенства на множители:\(\displaystyle (x-3)^2-5=(x-3-\sqrt{5})(x-3+\sqrt{5}){\small.}\)
\(\displaystyle (x-3)^2-5=(x-3)^2-(\sqrt{5})^2=(x-3-\sqrt{5})(x-3+\sqrt{5}) {\small.}\)
Исходное неравенство принимает вид:
\(\displaystyle (x-3-\sqrt{5})(x-3+\sqrt{5})< 0 {\small.}\)
Способ 1. Переход к системам линейных неравенств.
Все решения неравенства \(\displaystyle (x-3-\sqrt{5})(x-3+\sqrt{5})<0\) получаются, когда
- первый множитель положительный, второй отрицательный;
- первый множитель отрицательный, второй положительный.
Если это переписать в виде систем, то получаем:
\(\displaystyle \left\{\begin{aligned}x-3-\sqrt{5}&>0{ \small ,}\\x-3+\sqrt5 &< 0\end{aligned}\right.\) или \(\displaystyle \left\{\begin{aligned}x-3-\sqrt{5}&< 0{ \small ,}\\x-3+\sqrt5& >0{\small .}\end{aligned}\right.\)
Подробное решение систем линейных неравенств
\(\displaystyle \left\{\begin{aligned} x&>3+\sqrt{5}{ \small ,}\\ x&<3-\sqrt5 \end{aligned} \right.\) Неравенство \(\displaystyle x>3+\sqrt{5}\) соответствует множеству точек на прямой: 
Неравенство \(\displaystyle x<3-\sqrt5\) соответствует множеству точек на прямой:

Таким образом, переменная \(\displaystyle x\) одновременно больше \(\displaystyle 3+\sqrt5\) и меньше \(\displaystyle 3-\sqrt5{\small :}\)
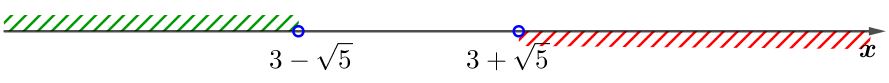
Так как в пересечении общих точек нет, то система неравенств решений не имеет. Значит, множество решений пусто. | или | \(\displaystyle \left\{\begin{aligned} x&<3+\sqrt{5}{ \small ,}\\ x&>3-\sqrt5 \end{aligned} \right.\) Неравенство \(\displaystyle x< 3+\sqrt5\) соответствует множеству точек на прямой: 
Неравенство \(\displaystyle x>3-\sqrt5\) соответствует множеству точек на прямой:

Таким образом, переменная \(\displaystyle x\) одновременно меньше \(\displaystyle 3+\sqrt5\) и больше \(\displaystyle 3-\sqrt5{\small :}\) 
Получившееся пересечение и будет решением исходной системы неравенств. Значит, решения – \(\displaystyle x\in (3-\sqrt5;3+\sqrt5){\small .} \) |
Объединяя решения систем, получаем:
\(\displaystyle x\in (3-\sqrt5;3+\sqrt5){\small .} \)
Ответ: \(\displaystyle x\in (3-\sqrt5;3+\sqrt5){\small .} \)
Способ 2. Графический.
Требуется решить неравенство:
\(\displaystyle (x-3-\sqrt{5})(x-3+\sqrt{5})< 0 {\small.}\)
Заметим, что при преобразовании выражения в левой части неравенства получится квадратный трехчлен с положительным коэффициентом при \(\displaystyle x^2{\small .}\)
\(\displaystyle (x-3-\sqrt{5})(x-3+\sqrt{5})=(x-3)^2-5=x^2-6x+4{\small .}\)
Значит, графиком функции \(\displaystyle y=(x-3-\sqrt{5})(x-3+\sqrt{5}) \) является парабола ветвями вверх.
Найдем точки пересечения параболы с осью \(\displaystyle \rm OX{\small ,} \) решив уравнение
\(\displaystyle (x-3-\sqrt{5})(x-3+\sqrt{5})=0{\small .} \)
Корни уравнения\(\displaystyle (x-3-\sqrt{5})(x-3+\sqrt{5})=0{\small :} \)\(\displaystyle x_{1}=3+\sqrt{5} {\small ,} \,\,x_{2}=3-\sqrt{5}{\small.}\)
Значит:
- либо \(\displaystyle x -3-\sqrt5=0{\small,}\) тогда \(\displaystyle x=3+\sqrt5{\small;}\)
- либо \(\displaystyle x -3+\sqrt5=0{\small,}\) откуда \(\displaystyle x=3-\sqrt5{\small.}\)
Для решения неравенства \(\displaystyle (x-3-\sqrt{5})(x-3+\sqrt{5}) \color{red}{<} 0 \) схематично изобразим график \(\displaystyle y=(x-3-\sqrt{5})(x-3+\sqrt{5})\)с учетом точек пересечения параболы с осью \(\displaystyle \rm OX \) и выделим красным цветом точки параболы, лежащие ниже оси \(\displaystyle \rm OX{ \small :} \)
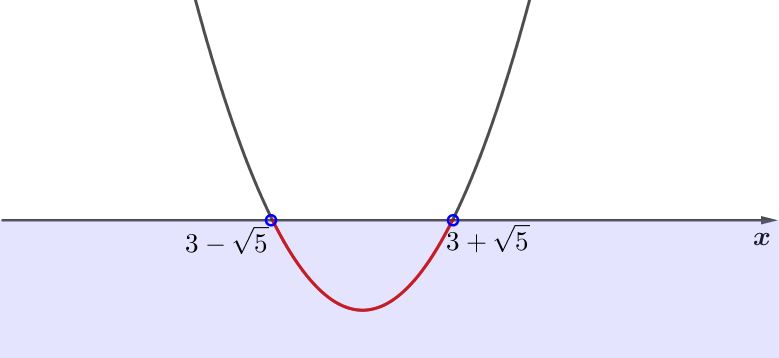
Следовательно, искомое решение – это все точки прямой между \(\displaystyle 3-\sqrt5\) и \(\displaystyle 3+\sqrt5{\small :}\)
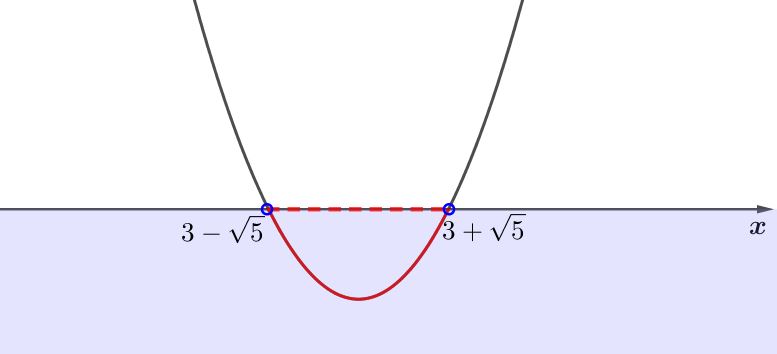
Получили решения – \(\displaystyle x \in (3-\sqrt{5};3+\sqrt{5}) {\small .} \)
Ответ: \(\displaystyle x \in (3-\sqrt{5};3+\sqrt{5}) {\small .}\)
Способ 3. Метод интервалов.
Решим исходное неравенство
\(\displaystyle \frac{-10}{(x-3)^2-5}\geqslant 0{\small.}\)
методом интервалов.
Используя формулу разности квадратов, разложим знаменатель на множители:\(\displaystyle (x-3)^2-5=(x-3-\sqrt{5})(x-3+\sqrt{5}){\small.}\)
\(\displaystyle (x-3)^2-5=(x-3)^2-(\sqrt{5})^2=(x-3-\sqrt{5})(x-3+\sqrt{5}) {\small.}\)
То есть исходное неравенство можно переписать в виде:
\(\displaystyle \frac{-10}{(x-3-\sqrt{5})(x-3+\sqrt{5})}\geqslant 0{\small.}\)
Необходимо найти корни знаменателя.
Корни знаменателя равны:
\(\displaystyle x_1=3-\sqrt{5} \) и \(\displaystyle x_2=3+\sqrt{5}{ \small .} \)
Расставим найденные корни на числовой оси.
Поскольку знак неравенства нестрогий, то
- все нули числителя, которые не обращают в ноль знаменатель, обозначаются закрашенными;
- все нули знаменателя всегда обозначаются выколотыми.
Так как обе точки \(\displaystyle x=3-\sqrt{5} \) и \(\displaystyle x=3+\sqrt{5} \) обращают в ноль знаменатель, то они обозначаются выколотыми.
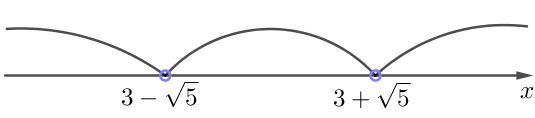
Получили три интервала:
\(\displaystyle (-\infty;3-\sqrt{5}){ \small ,} \, (3-\sqrt{5};3+\sqrt{5})\) и \(\displaystyle (3+\sqrt{5};+\infty){\small .}\)
Определим знак функции \(\displaystyle f(x)=\frac{-10}{(x-3-\sqrt{5})(x-3+\sqrt{5})}\) на каждом из интервалов.
Определим знак функции \(\displaystyle f(x)=\frac{-10}{(x-3-\sqrt{5})(x-3+\sqrt{5})}\) на каждом из интервалов.
Замечание / комментарийТак как \(\displaystyle 2=\sqrt{4}{\small ,} \) \(\displaystyle 3=\sqrt{9}{\small ,} \) то
\(\displaystyle 2<\sqrt{5}<3\) и \(\displaystyle -3<-\sqrt{5}<-2{\small .}\)
Прибавив \(\displaystyle 3\) к обеим частям полученных неравенств, получаем:
\(\displaystyle 5<3+\sqrt{5}<6\) и \(\displaystyle 0<3-\sqrt{5}<1{\small .}\)
Для интервала \(\displaystyle (-\infty;3-\sqrt{5})\) выберем \(\displaystyle x=-10{\small :}\)
\(\displaystyle f(-1)=\frac{-10}{(-10-3-\sqrt{5})(-10-3+\sqrt{5})}<0{\small .}\)
Пишем знак минус в интервале \(\displaystyle (-\infty;3-\sqrt{5}){\small.}\)
Для интервала \(\displaystyle (3-\sqrt{5};3+\sqrt{5})\) выберем \(\displaystyle x=3{\small :}\)
\(\displaystyle f(1)=\frac{-10}{(3-3-\sqrt{5})(3-3+\sqrt{5})}>0{\small .}\)
Пишем знак плюс в интервале \(\displaystyle (3+\sqrt{5};3+\sqrt{5}){\small .}\)
Для интервала \(\displaystyle (3+\sqrt{5};+\infty)\) выберем \(\displaystyle x=10{\small :}\)
\(\displaystyle f(4)=\frac{-10}{(10-3-\sqrt{5})(10-3+\sqrt{5})}<0{\small .}\)
Пишем знак минус в интервале \(\displaystyle (3+\sqrt{5};+\infty){\small .}\)
В итоге получаем:
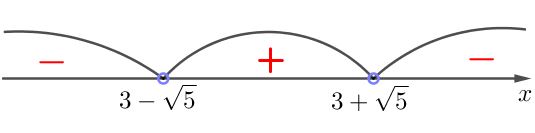
Так как решения неравенства \(\displaystyle \frac{-10}{(x-3-\sqrt{5})(x-3+\sqrt{5})} \geqslant 0\) соответствуют промежуткам, где функция положительна, и невыколотым точкам, являющимся концами промежутков (в данном случае таких точек нет), то
\(\displaystyle (3-\sqrt{5};3+\sqrt{5})\) – искомое решение.
Ответ: \(\displaystyle x \in (3-\sqrt{5};3+\sqrt{5}) {\small .}\)