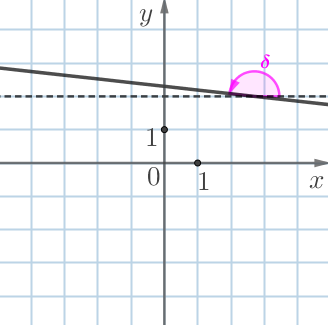
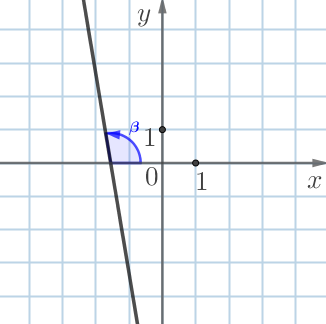
На рисунках изображены графики функций вида \(\displaystyle y=kx+b \small .\)
Установите соответствие между графиками линейных функций и угловыми коэффициентами прямых.
ГРАФИКИ
| \(\displaystyle А\) | \(\displaystyle Б\) |
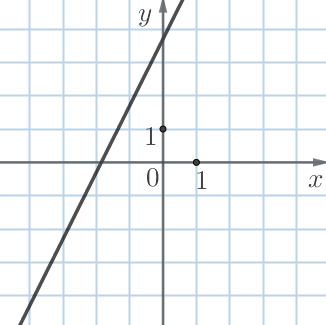 | 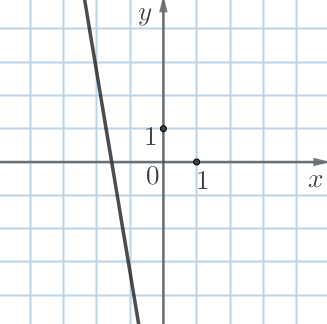 |
| \(\displaystyle В\) | \(\displaystyle Г\) |
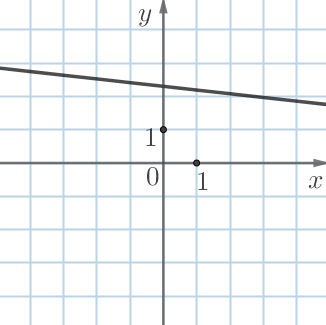 | 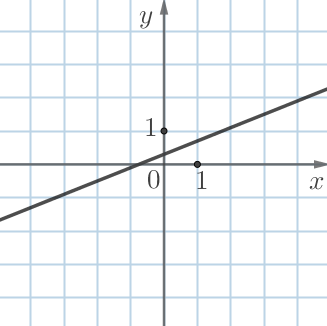 |
УГЛОВЫЕ КОЭФФИЦИЕНТЫ
\(\displaystyle 1)\) \(\displaystyle 2 {\small;}\) \(\displaystyle 2)\) \(\displaystyle 0 {, }4 {\small;}\) \(\displaystyle 3)\) \(\displaystyle -6{\small;}\) \(\displaystyle 4)\) \(\displaystyle -\dfrac{1}{9}{\small.}\)
В таблице под каждой буквой укажите соответствующий номер.
| \(\displaystyle А\) | \(\displaystyle Б\) | \(\displaystyle В\) | \(\displaystyle Г\) |
Даны четыре графика линейных функций \(\displaystyle y=kx+b\) и четыре угловых коэффициента: два отрицательных и два положительных.
Требуется установить какой угловой коэффициент соответствует каждому графику.
Сделаем это, сравнив угловые коэффициенты прямых по графикам.
1. Найдём сначала знаки угловых коэффициентов.
Угловые коэффициенты прямых \(\displaystyle Б\) и \(\displaystyle В\) отрицательны.
Определим по графикам возрастают или убывают соответствующие функции и найдём знаки угловых коэффициентов.
| \(\displaystyle А\) | \(\displaystyle Б\) | \(\displaystyle В\) | \(\displaystyle Г\) |
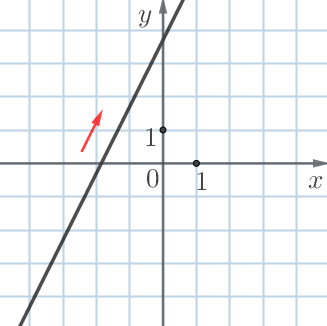 | 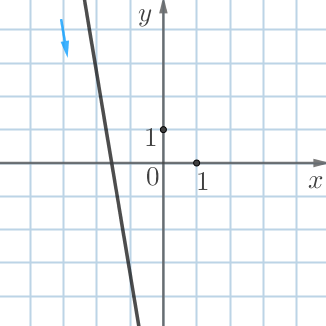 | 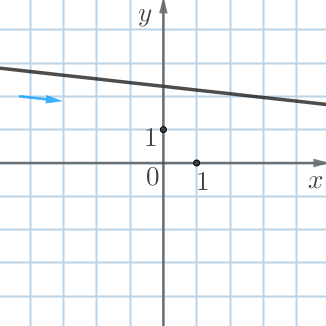 | 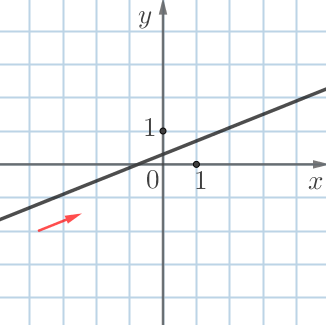 |
| возрастает | убывает | убывает | возрастает |
| \(\displaystyle k>0\) | \(\displaystyle k<0\) | \(\displaystyle k<0\) | \(\displaystyle k>0\) |
Таким образом, получаем:
- угловые коэффициенты прямых \(\displaystyle А\) и \(\displaystyle Г\) положительны,
- угловые коэффициенты прямых \(\displaystyle Б\) и \(\displaystyle В {\small }\) отрицательны.
2. Установим соответствие между прямыми \(\displaystyle А\) и \(\displaystyle Г\) и положительными угловыми коэффициентами \(\displaystyle k=2 {\small }\) и \(\displaystyle k=0{,}4 {\small .}\)
Графику \(\displaystyle Г\) соответствует \(\displaystyle k=0{,}4 {\small }\) под номером \(\displaystyle 2 {\small . }\)
Угловой коэффициент прямой \(\displaystyle y=kx+b {\small }\) равен тангенсу угла между этой прямой и положительным направлением оси \(\displaystyle Ox{\small.}\)
Поэтому достаточно сравнить тангенсы соответствующих углов.
Обе прямые образуют острые углы с положительным направлением оси \(\displaystyle Ox{\small.}\)
Воспользуемся тем, что в этом случае чем больше угол наклона, тем больше его тангенс.
| \(\displaystyle А\) | \(\displaystyle Г\) |
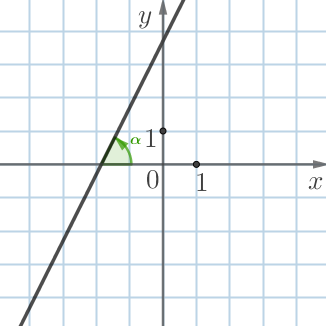 | 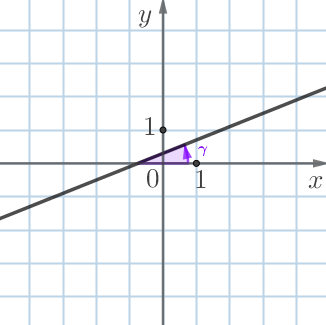 |
Угол \(\displaystyle \color{#339900}{\alpha}\) наклона прямой \(\displaystyle А\) больше, чем угол \(\displaystyle \color{#7F00FF}{\gamma}\) наклона прямой \(\displaystyle Г{\small .}\)
Значит, тангенс угла \(\displaystyle \color{#339900}{\alpha}\) больше, чем тангенс угла \(\displaystyle \color{#7F00FF}{\gamma}{\small.}\)
Следовательно, угловой коэффициент прямой \(\displaystyle А\) больше, чем угловой коэффициент прямой \(\displaystyle Г {\small .}\)
Тогда
- прямой \(\displaystyle А\) соответствует угловой коэффициент \(\displaystyle k=2 {\small }\) под номером \(\displaystyle 1 {\small ; }\)
- прямой \(\displaystyle Г\) соответствует \(\displaystyle k=0{,}4 {\small }\) под номером \(\displaystyle 2 {\small . }\)
3. Установим соответствие между прямыми \(\displaystyle Б\) и \(\displaystyle В\) и отрицательными угловыми коэффициентами
\(\displaystyle k=-6 {\small }\) и \(\displaystyle k=-\dfrac{1}{9} {\small .}\)
Графику\(\displaystyle В\) соответствует \(\displaystyle k=-\dfrac{1}{9} {\small }\) под номером \(\displaystyle 4 {\small . }\)
Занесём полученные результаты в таблицу.
Ответ:
| \(\displaystyle А\) | \(\displaystyle Б\) | \(\displaystyle В\) | \(\displaystyle Г\) |
| \(\displaystyle 1\) | \(\displaystyle 3\) | \(\displaystyle 4\) | \(\displaystyle 2\) |