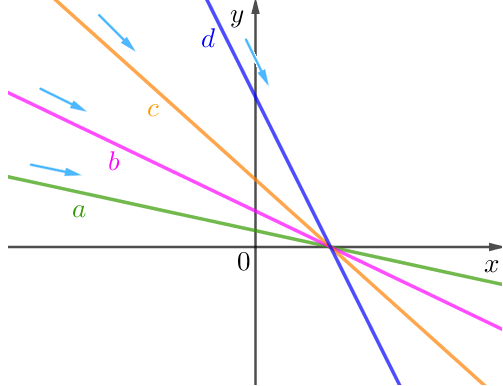
На рисунке изображены четыре прямые – графики линейных функций \(\displaystyle y=kx+b {\small .}\)
Расположите данные прямые в порядке убывания их угловых коэффициентов.
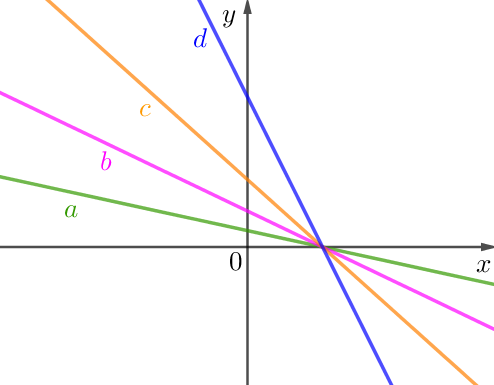
1. Определим сначала знаки угловых коэффициентов.
Получили угловые коэффициенты одного знака, поэтому сразу сделать вывод о том, какой из них меньше, не можем.
2. Вспомним правило:
Угловой коэффициент прямой \(\displaystyle y=kx+b {\small }\) равен тангенсу угла между этой прямой и положительным направлением оси \(\displaystyle Ox{\small.}\)
и сравним тангенсы соответствующих углов.
Все прямые образуют тупые углы с положительным направлением оси \(\displaystyle Ox{\small:}\)
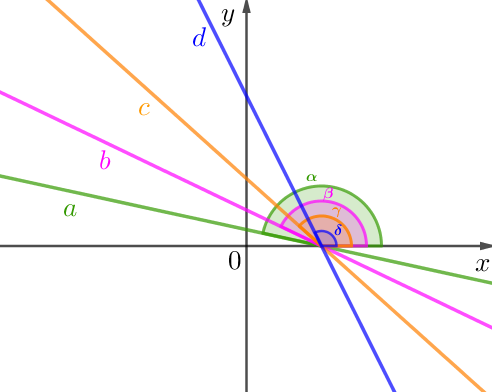
Воспользуемся правилом:
Если прямая образует тупой угол с положительным направлением оси \(\displaystyle \rm OX{\small,}\) то
чем меньше угол наклона, тем меньше тангенс.
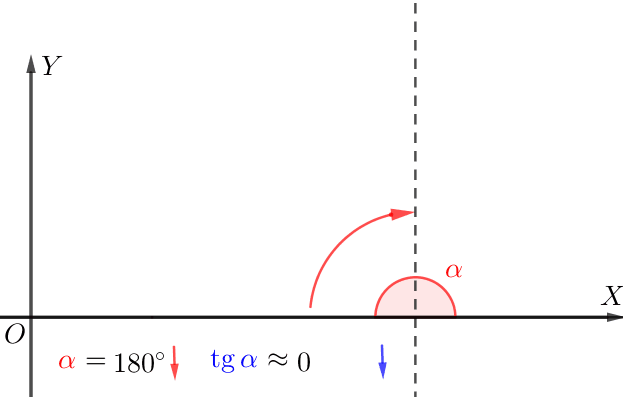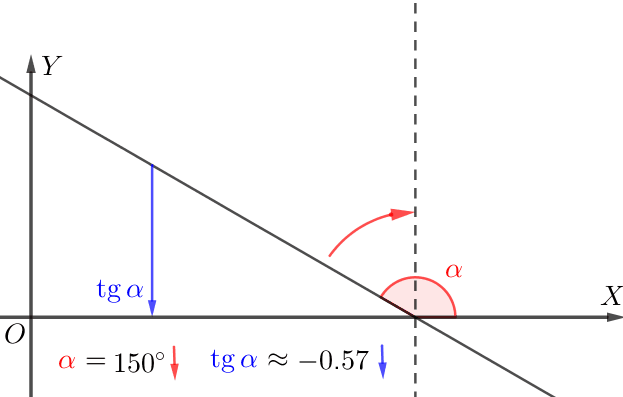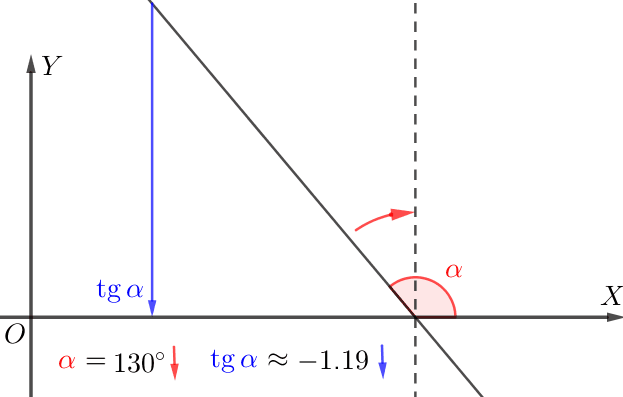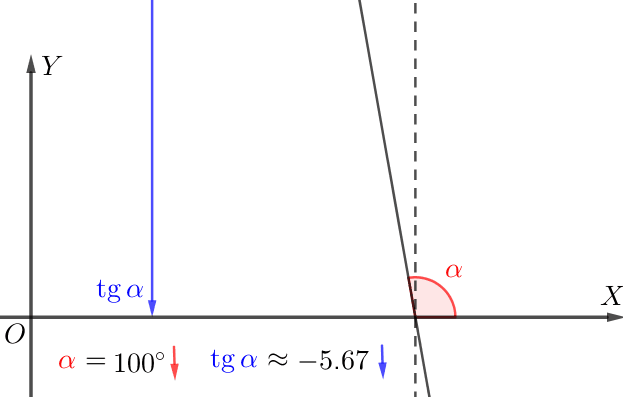
Видим по рисунку, что:
\(\displaystyle \color{Blue}{\delta}<\color{#FF7F00}{\gamma}<\color{magenta} {\beta}<\color{#339900}{\alpha}{\small.}\)
Значит,
\(\displaystyle \tg \color{Blue}{\delta}< \tg \color{#FF7F00}{\gamma}< \tg \color{magenta} {\beta}<\tg \color{#339900}{\alpha}{\small.}\)
Следовательно,
\(\displaystyle \color{Blue}{k_d}<\color{#FF7F00}{k_c}<\color{magenta} {k_b}<\color{#339900}{k_a}{\small.}\)
В ответе требуется расположить прямые в порядке убывания угловых коэффициентов: от самого большого к самому маленькому.
Ответ: \(\displaystyle \color{#339900}{a} {\small,} \, \, \color{magenta} {b} {\small,} \, \, \color{#FF7F00}{c} {\small,} \, \, \color{Blue}{d} {\small.}\)