Укажите неравенство, которое не имеет решений.
Надо выяснить, какое из данных неравенств не имеет решений.
Решим каждое из неравенств.
Решим неравенство
\(\displaystyle x^2+3x+25< 0{\small .}\)
Сначала решим квадратное уравнение \(\displaystyle x^2+3x+25=0{\small .}\)
Для квадратного уравнения \(\displaystyle x^2+3x +25=0\) дискриминант
\(\displaystyle {\rm D}= 3^2-4\cdot 1\cdot 25=-91<0{\small .}\)
Так как дискриминант отрицателен, то уравнение не имеет решений в действительных числах.
Значит, нужно рассматривать всю числовую ось как один промежуток:

Получаем один интервал:
\(\displaystyle (-\infty;+\infty){\small .}\)
При этом на всей числовой прямой функция \(\displaystyle f(x)=x^2+3x+25\) будет иметь один знак.
Выберем любую точку на прямой и определим знак функции в данной точке. Наиболее удобно выбрать \(\displaystyle x=0{\small :}\)
\(\displaystyle f(0)=0^2+2\cdot 0 +25=25>0{\small .}\)
Пишем знак плюс в интервале \(\displaystyle (-\infty;+\infty){\small :}\)

Решения неравенства \(\displaystyle x^2+3x+25<0\) соответствуют промежуткам, где функция \(\displaystyle f(x)=x^2+3x+25\) отрицательна.
Так как функция \(\displaystyle f(x)=x^2+3x+25\) всюду положительна, то решений нет, то есть
\(\displaystyle \varnothing\) – искомое решение.
Решим неравенство
\(\displaystyle x^2+3x-35> 0{ \small .} \)
Решим квадратное уравнение
\(\displaystyle x^2+3x-35=0{ \small .} \)
Вычислим дискриминант:
\(\displaystyle {\rm D}= 3^2-4\cdot 1\cdot (-35)=9+100=109\)
и
\(\displaystyle \sqrt{\rm D}=\sqrt{ 109}=\sqrt{ 109}{\small .} \)
Найдем корни уравнения:
\(\displaystyle x_1= \frac{-3-\sqrt{ 109}}{2}{ \small ,}\)
\(\displaystyle x_2=\frac{-3+\sqrt{ 109}}{2}{\small .}\)
Отметим найденные корни на числовой прямой, выкалывая их (так как знак неравенства строгий):
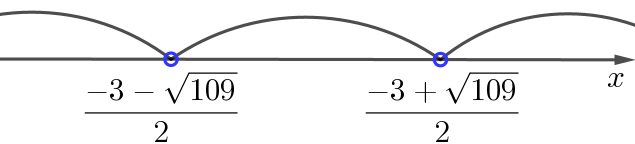
Получили три интервала:
\(\displaystyle \left(-\infty;\frac{-3-\sqrt{ 109}}{2}\right){ \small ,} \, \left(\frac{-3-\sqrt{ 109}}{2};\frac{-3+\sqrt{ 109}}{2}\right)\) и \(\displaystyle \left(\frac{-3+\sqrt{ 109}}{2};+\infty\right){\small .}\)
Определим знак функции \(\displaystyle f(x)={ x^2+3x - 25}\) на каждом из интервалов.
Для интервала \(\displaystyle \left(-\infty;\frac{-3-\sqrt{ 109}}{2}\right)\) выберем \(\displaystyle x=-7{\small :}\)
\(\displaystyle f(-7)={ (-7)^2 +3\cdot (-7) - 25 }>0{\small .}\)
Пишем знак плюс в интервале \(\displaystyle \left(-\infty;\frac{-3-\sqrt{ 109}}{2}\right){\small.}\)
Для интервала \(\displaystyle \left(\frac{-3-\sqrt{ 109}}{2};\frac{-3+\sqrt{ 109}}{2}\right)\) выберем \(\displaystyle x=0{\small :}\)
\(\displaystyle f(0)={ 0^2+3\cdot 0 - 25 }<0{\small .}\)
Пишем знак минус в интервале \(\displaystyle \left(\frac{-3-\sqrt{ 109}}{2};\frac{-3+\sqrt{ 109}}{2}\right){\small .}\)
Для интервала \(\displaystyle \left(\frac{-3+\sqrt{ 109}}{2};+\infty\right)\) выберем \(\displaystyle x=7{\small :}\)
\(\displaystyle f(7)={ 7^2 +3\cdot 7 - 25 }>0{\small .}\)
Пишем знак плюс в интервале \(\displaystyle \left(\frac{-3+\sqrt{ 109}}{2};+\infty\right){\small .}\)
В итоге получаем:
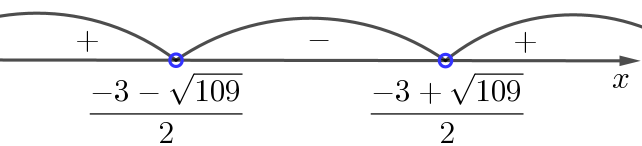
Так как решения неравенства \(\displaystyle x^2+3x-35> 0{\small } \) соответствуют промежуткам, где функция положительна, то
\(\displaystyle \left(-\infty;\frac{-3-\sqrt{ 109}}{2}\right)\cup\left(\frac{-3+\sqrt{ 109}}{2};+\infty\right)\) – искомое решение.
Решим неравенство
\(\displaystyle x^2+3x+25> 0{\small .}\)
Сначала решим квадратное уравнение \(\displaystyle x^2+3x+25=0{\small .}\)
Для квадратного уравнения \(\displaystyle x^2+3x +25=0\) дискриминант
\(\displaystyle {\rm D}= 3^2-4\cdot 1\cdot 25=-91<0{\small .}\)
Так как дискриминант отрицателен, то уравнение не имеет решений в действительных числах.
Значит, нужно рассматривать всю числовую ось как один промежуток:

Получаем один интервал:
\(\displaystyle (-\infty;+\infty){\small .}\)
При этом на всей числовой прямой функция \(\displaystyle f(x)=x^2+3x+25\) будет иметь один знак.
Выберем любую точку на прямой и определим знак функции в данной точке. Наиболее удобно выбрать \(\displaystyle x=0{\small :}\)
\(\displaystyle f(0)=0^2+3\cdot 0 +25=25>0{\small .}\)
Пишем знак плюс в интервале \(\displaystyle (-\infty;+\infty){\small :}\)

Так как решения неравенства \(\displaystyle x^2+3x+25>0\) соответствуют промежуткам, где функция \(\displaystyle f(x)=x^2+3x+25\) положительна, то
\(\displaystyle (-\infty;+\infty)\) – искомое решение.
Решим неравенство
\(\displaystyle x^2+3x-35< 0{ \small .} \)
Решим квадратное уравнение
\(\displaystyle x^2+3x-35=0{ \small .} \)
Вычислим дискриминант:
\(\displaystyle {\rm D}= 3^2-4\cdot 1\cdot (-35)=9+100=109\)
и
\(\displaystyle \sqrt{\rm D}=\sqrt{ 109}=\sqrt{ 109}{\small .} \)
Найдем корни уравнения:
\(\displaystyle x_1= \frac{-3-\sqrt{ 109}}{2}{ \small ,}\)
\(\displaystyle x_2=\frac{-3+\sqrt{ 109}}{2}{\small .}\)
Отметим найденные корни на числовой прямой, выкалывая их (так как знак неравенства строгий):
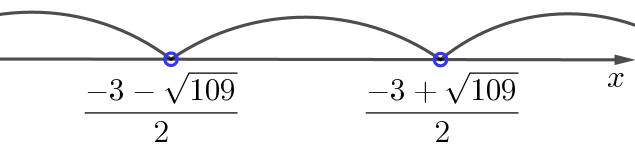
Получили три интервала:
\(\displaystyle \left(-\infty;\frac{-3-\sqrt{ 109}}{2}\right){ \small ,} \, \left(\frac{-3-\sqrt{ 109}}{2};\frac{-3+\sqrt{ 109}}{2}\right)\) и \(\displaystyle \left(\frac{-3+\sqrt{ 109}}{2};+\infty\right){\small .}\)
Определим знак функции \(\displaystyle f(x)={ x^2+3x - 25}\) на каждом из интервалов.
Для интервала \(\displaystyle \left(-\infty;\frac{-3-\sqrt{ 109}}{2}\right)\) выберем \(\displaystyle x=-7{\small :}\)
\(\displaystyle f(-7)={ (-7)^2 +2\cdot (-7) - 25 }>0{\small .}\)
Пишем знак плюс в интервале \(\displaystyle \left(-\infty;\frac{-3-\sqrt{ 109}}{2}\right){\small.}\)
Для интервала \(\displaystyle \left(\frac{-3-\sqrt{ 109}}{2};\frac{-3+\sqrt{ 109}}{2}\right)\) выберем \(\displaystyle x=0{\small :}\)
\(\displaystyle f(0)={ 0^2+2\cdot 0 - 25 }<0{\small .}\)
Пишем знак минус в интервале \(\displaystyle \left(\frac{-3-\sqrt{ 109}}{2};\frac{-3+\sqrt{ 109}}{2}\right){\small .}\)
Для интервала \(\displaystyle \left(\frac{-3+\sqrt{ 109}}{2};+\infty\right)\) выберем \(\displaystyle x=7{\small :}\)
\(\displaystyle f(7)={ 7^2 +2\cdot 7 - 25 }>0{\small .}\)
Пишем знак плюс в интервале \(\displaystyle \left(\frac{-3+\sqrt{ 109}}{2};+\infty\right){\small .}\)
В итоге получаем:
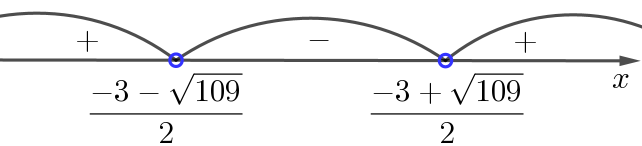
Так как решения неравенства \(\displaystyle x^2+3x-35> 0{\small } \) соответствуют промежуткам, где функция отрицательна, то
\(\displaystyle \left(\frac{-3-\sqrt{ 109}}{2};\frac{-3+\sqrt{ 109}}{2}\right)\) – искомое решение.
Правильный ответ указан под номером \(\displaystyle 1{\small . }\)
Ответ: \(\displaystyle 1{\small . }\)