Постройте график функции
\(\displaystyle y=|x^2+2x-3|\small.\)
Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?
Наибольшее число общих точек равно
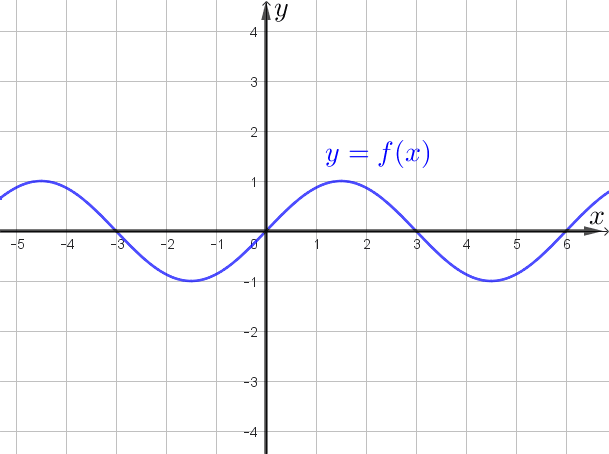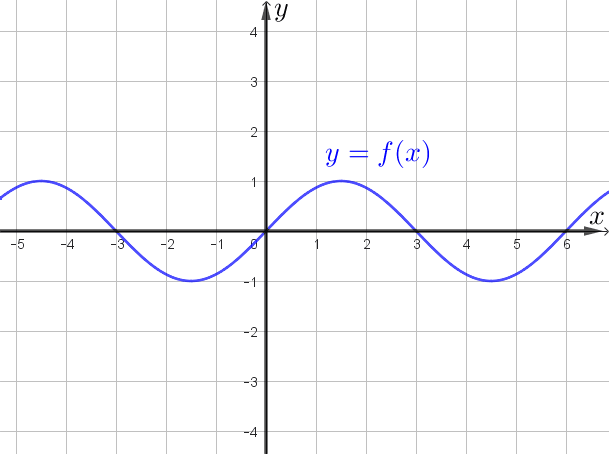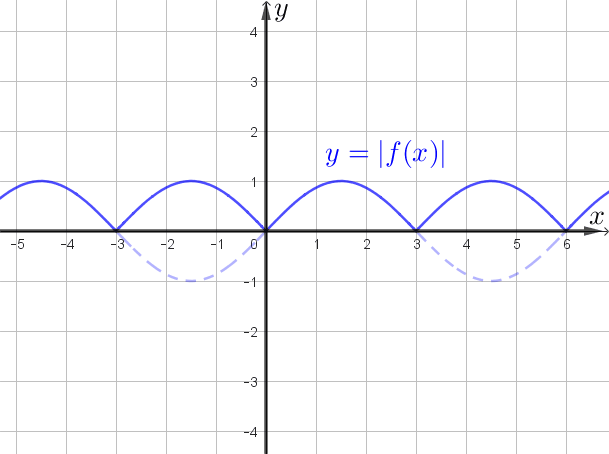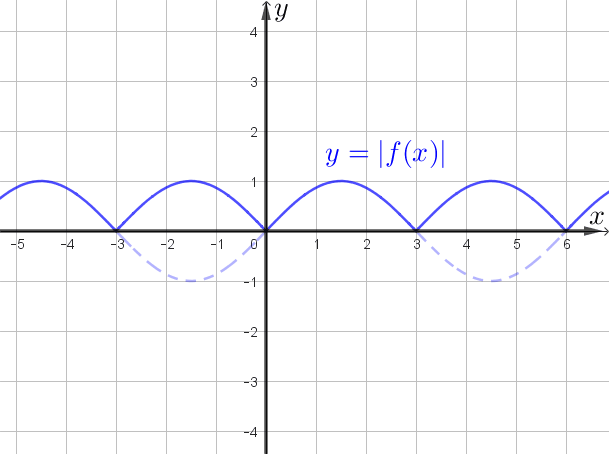
- нужно построить график функции \(\displaystyle y=f(x)\small,\)
- все части графика, которые ниже оси абсцисс, отразить относительно нее.
Значит, для построения графика функции \(\displaystyle y=|x^2+2x-3|\) необходимо:
- построить параболу \(\displaystyle y=x^2+2x-3\small,\)
- все части графика, которые ниже оси абсцисс, отразить относительно этой оси.
Строим параболу \(\displaystyle y=x^2+2x-3\) по вершине и точке.
Напомним, как найти абсциссу вершины параболы:
Абсцисса вершины параболы
Абсцисса \(\displaystyle x_0\) вершины параболы \(\displaystyle y=\color{red}ax^2+\color{blue}bx+\color{green}c\) находится по формуле:
\(\displaystyle x_0=\frac{-\color{blue}b}{2\color{red}a}{\small.}\)
Тогда абсцисса вершины параболы \(\displaystyle y=x^2+2x-3{\small:}\)
\(\displaystyle x_0=\frac{-2}{2\cdot1}=-1{\small.}\)
Подставляя абсциссу \(\displaystyle -1\) в уравнение параболы, найдем ординату вершины:
\(\displaystyle y_0=(-1)^2+2\cdot(-1)-3=-4\small.\)
Найдем координаты еще какой-нибудь точки на параболе.
Например, возьмем точку с абсциссой \(\displaystyle x=0{\small.}\) Тогда ее ордината:
\(\displaystyle y=0^2+2\cdot0-3=-3{\small.}\)
Строим параболу по вершине и точке:
Отметим также, что и дискриминант квадратного уравнения \(\displaystyle y=x^2+2x-3\) равен
\(\displaystyle {\rm D}=2^2-4\cdot(-3)=16\small.\)
Значит, корни:
\(\displaystyle x_1=\frac{-2+\sqrt{16}}{2}=1\small,\)
\(\displaystyle x_2=\frac{-2-\sqrt{16}}{2}=-3\small.\)
То есть парабола пересекает ось абсцисс в точках \(\displaystyle 1\) и \(\displaystyle -3\small.\)
Отражая все точки, которые ниже оси абсцисс относительно этой оси, получаем:
Это график функции \(\displaystyle y=|x^2+2x-3|\small.\)
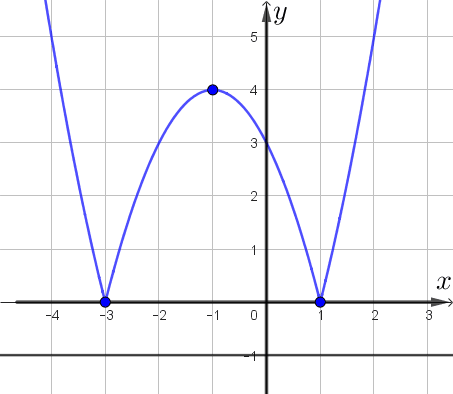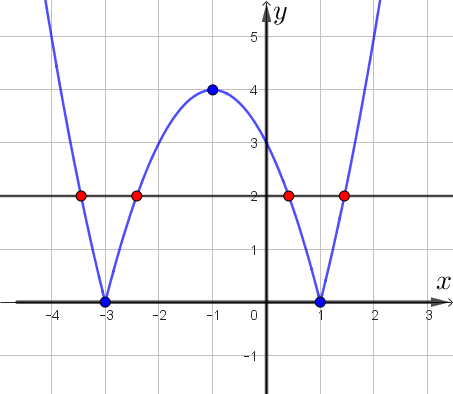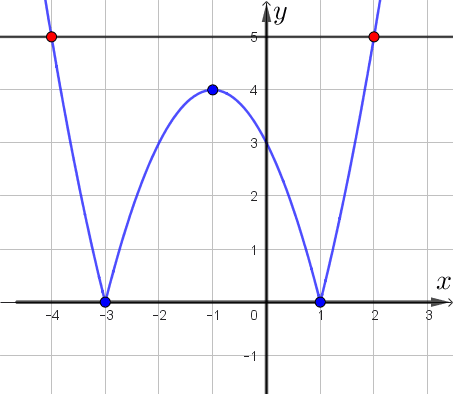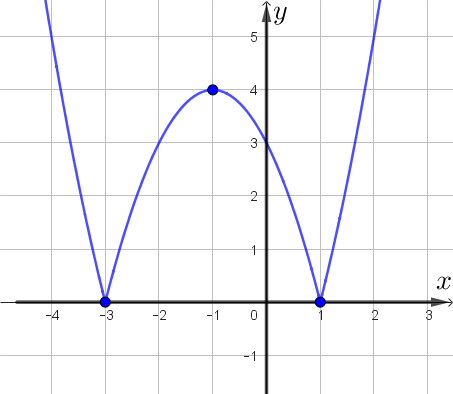
Получаем, что прямая, параллельная оси абсцисс, имеет \(\displaystyle 4\small,\) \(\displaystyle 3\) или \(\displaystyle 2\) общие точки с графиком, либо не имеет общих точек.
Таким образом, наибольшее число общих точек графика с прямой, параллельной оси абсцисс, равно \(\displaystyle 4\small.\)
Ответ: \(\displaystyle 4\small.\)