Постройте график функции
\(\displaystyle y=|x^2-4|\)
Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?
Наибольшее число общих точек равно
Чтобы построить график \(\displaystyle y=|x^2-4|\small,\) раскроем модуль.
\(\displaystyle y=\begin{cases}x^2-4, \,\,{\small при}\,\,x\leqslant-2\,\, {\small или}\,\,x\geqslant 2 ,\\-x^2+4,\,\,{\small при}\,\,-2< x<2.\end{cases}\)
Чтобы раскрыть модуль, решим неравенство \(\displaystyle x^2-4\geqslant0\) метод интервалов.
1. Корни уравнения \(\displaystyle x^2-4=0\) – это
\(\displaystyle x_1=-2\) и \(\displaystyle x_2=2\small.\)
2. Отметим закрашенными (так как знак неравенства нестрогий) точками найденные корни на числовой прямой:
Получаем три интервала.
3. Проверим знак выражения \(\displaystyle x^2-4\) на каждом из них:
- для \(\displaystyle x=-3\) получаем: \(\displaystyle (-3)^2-4=5>0\small;\)
- для \(\displaystyle x=0\) получаем: \(\displaystyle 0^2-4=-4<0\small;\)
- для \(\displaystyle x=3\) получаем: \(\displaystyle 3^2-4=5>0\small.\)
Получаем:
Значит,
- при \(\displaystyle x\leqslant-2\) или \(\displaystyle x\geqslant 2\) выражение \(\displaystyle x^2-4\geqslant0\) и
\(\displaystyle |x^2-4|=x^2-4\small;\)
- при \(\displaystyle -2< x<2\) выражение \(\displaystyle x^2-4<0\) и
\(\displaystyle |x^2-4|=-(x^2-4)=-x^2+4\small.\)
Построим график кусочно-заданной функции
\(\displaystyle y=\begin{cases}x^2-4, \,\,{\small при}\,\,x\leqslant-2\,\, {\small или}\,\,x\geqslant 2 ,\\-x^2+4,\,\,{\small при}\,\,-2< x<2\end{cases}\)
по шагам:
- сначала построим график \(\displaystyle y=x^2-4 \) для \(\displaystyle x\leqslant-2\) или \(\displaystyle x\geqslant 2\small,\)
- затем построим график \(\displaystyle y=-x^2+4\) для \(\displaystyle -2< x<2\small.\)
\(\displaystyle y=\begin{cases} x^2-4, \,\,{\small при}\,\,x\leqslant-2\,\, {\small или}\,\,x\geqslant 2 ,\\ -x^2+4,\,\,{\small при}\,\,-2< x<2. \end{cases} \) |
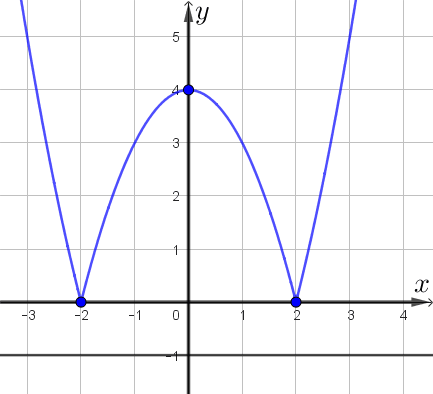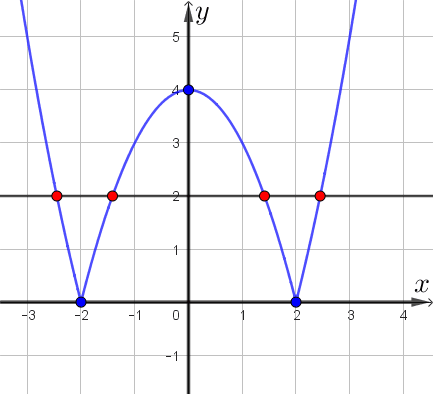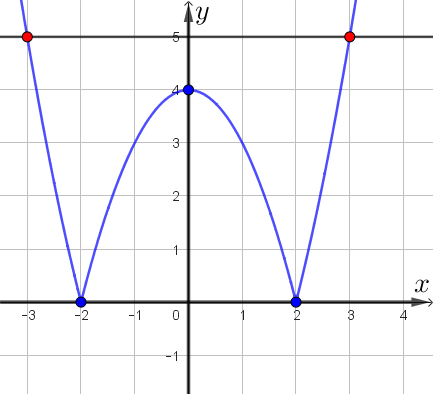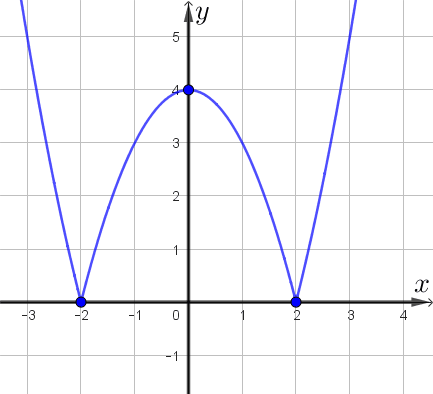
Получаем, что прямая, параллельная оси абсцисс, имеет \(\displaystyle 4\small,\) \(\displaystyle 3\) или \(\displaystyle 2\) общие точки с графиком, либо не имеет общих точек.
Таким образом, наибольшее число общих точек графика с прямой, параллельной оси абсцисс, равно \(\displaystyle 4\small.\)
Ответ: \(\displaystyle 4\small.\)