Skip to main content

Теория: Горизонтальная прямая

Задание

Постройте график функции 

\(\displaystyle y=3-\frac{x+2}{x^2+2x}\small.\)

Определите, при каких значениях \(\displaystyle m\) прямая \(\displaystyle y=m\) не имеет с графиком общих точек.

Решение

Информация

Если дробь \(\displaystyle \frac{x+2}{x^2+2x}\) просто сократить, то получим

\(\displaystyle \frac{x+2}{x^2+2x}=\frac{1}{x}\)

При этом левая и правая части выражения имеют разные области допустимых значений:

  • дробь \(\displaystyle \frac{x+2}{x^2+2x}\)не определена при \(\displaystyle x=0\) и \(\displaystyle x=-2{\small ; } \)
  • дробь \(\displaystyle \frac{1}{x}\)не определена при \(\displaystyle x=0\small.\)

Равенство выражений имеет место только для тех \(\displaystyle x\small,\) для которых определены оба выражения.

Поэтому нужно обязательно записать область определения исходной функции.

Область определения функции \(\displaystyle y=3-\frac{x+2}{x^2+2x}{\small:}\)

\(\displaystyle x\,\cancel{=}\,0\) и \(\displaystyle x\,\cancel{=}\,-2\small.\)

Знаменатель дроби не равен \(\displaystyle 0{\small:}\)

\(\displaystyle x^2+2x\,\cancel{=}\,0,\)

\(\displaystyle x(x+2)\,\cancel{=}\,0,\)

\(\displaystyle x\,\cancel{=}\,0\) и \(\displaystyle x\,\cancel{=}\,-2\small.\)

В области определения исходного выражения получаем:

\(\displaystyle 3-\frac{x+2}{x^2+2x}=3-\frac{\cancel{x+2}}{x\cancel{(x+2)}}=3-\frac{1}{x}\small.\)

Тогда, с учетом области определения исходного выражения, необходимо построить гиперболу с выколотой точкой при \(\displaystyle x=-2\small:\)

\(\displaystyle \begin{cases}y=3-\dfrac{1}{x},\\x\,\cancel{=}\,-2.\end{cases}\)

И определить, при каких значениях параметра \(\displaystyle k\) прямая \(\displaystyle y=m\) не имеет с графиком общих точек.

Построим график функции \(\displaystyle y=3-\dfrac{1}{x}\) для \(\displaystyle x\,\cancel{=}\,-2\small.\)

1. Строим гиперболу \(\displaystyle y=3-\dfrac{1}{x}\small.\)

Это гипербола \(\displaystyle y=-\dfrac{1}{x}{ \small ,}\) сдвинутая на \(\displaystyle 3\) единицы вверх.

2. Так как \(\displaystyle x\,\cancel{=}\,-2\small,\) выкалываем на графике точку с абсциссой \(\displaystyle x=-2\small.\)

(Точек с абсциссой \(\displaystyle x=0\) на гиперболе нет.)

Отметим, что выколотая точка имеет координаты \(\displaystyle (-2;\,3{,}5)\small.\)

Определим, при каких значениях \(\displaystyle m\) прямая \(\displaystyle y=m\) не имеет с графиком общих точек.

Прямая \(\displaystyle y=m\) – горизонтальная прямая.

Горизонтальная прямая не имеет точек пересечения с построенным графиком, если

  • эта прямая – горизонтальная асимптота,
  • эта прямая проходит через выколотую точку графика.

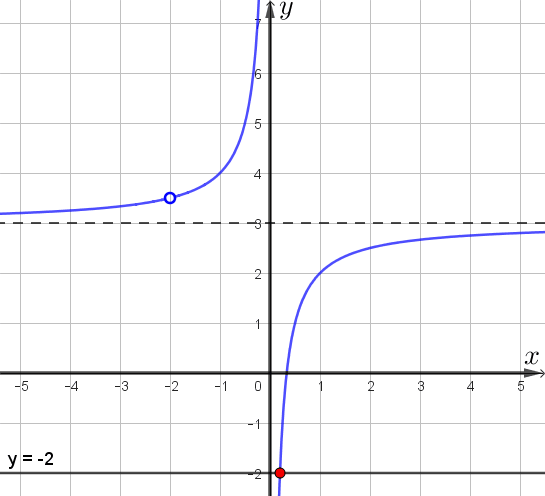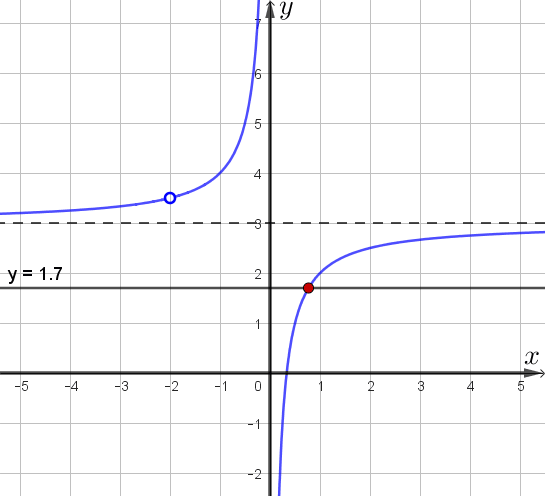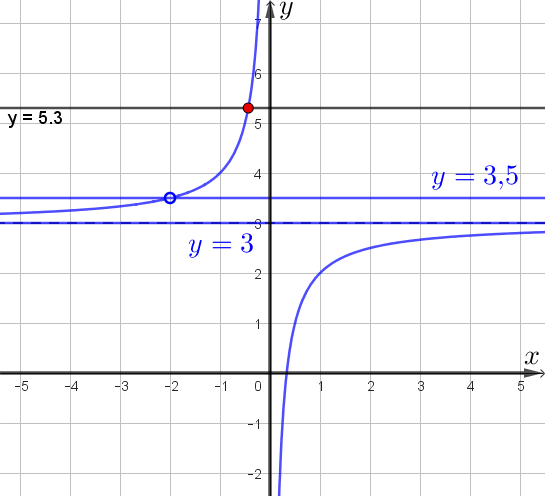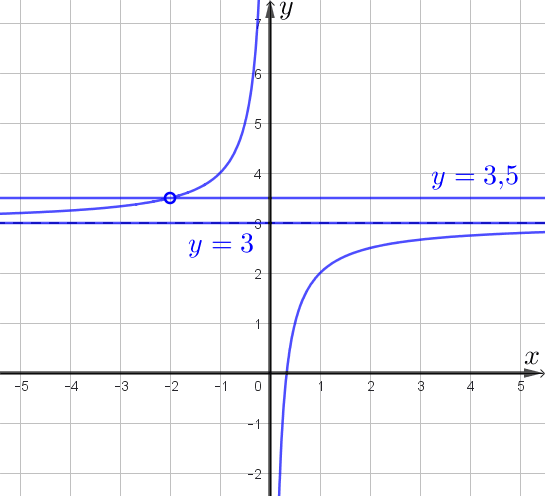
Таким образом, прямая \(\displaystyle y=m\) не имеет с графиком общих точек при

\(\displaystyle m\in\{ 3\}\cup\{3{,}5\}\small.\)

Ответ: \(\displaystyle m\in\{ 3\}\cup\{3{,}5\}\small.\)